计算机图形表面

多边形表面

对象表示为表面的集合。3D 对象表示分为两类。

• 边界表示 (B-reps) − 它将 3D 对象描述为一组将对象内部与环境分隔开的表面。

• 空间分区表示 − 它用于描述内部属性，通过将包含对象的空间区域划分为一组小的、不重叠的连续实体（通常是立方体）。

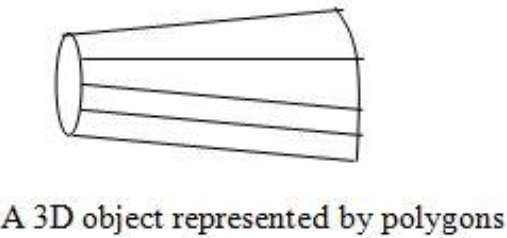
3D 图形对象最常用的边界表示是一组包围对象内部的表面多边形。许多图形系统都使用此方法。存储一组多边形以进行对象描述。这简化并加快了物体的表面渲染和显示，因为所有表面都可以用线性方程来描述。

多边形表面在设计和实体建模应用中很常见，因为它们的线框显示可以快速完成，以给出表面结构的一般指示。然后通过在多边形表面上插入阴影图案来产生逼真的场景以进行照明。

多边形表

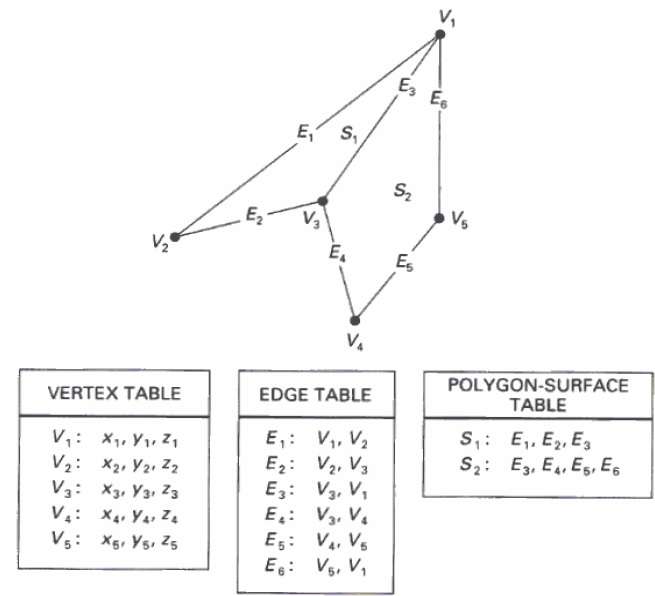
在此方法中，表面由一组顶点坐标和相关属性指定。如下图所示，有五个顶点，从 v₁ 到 v₅。

• 每个顶点存储 x、y 和 z 坐标信息，在表中表示为 v₁：x₁、y₁、z₁。

• 边表用于存储多边形的边信息。在下图中，边 E₁ 位于顶点 v₁ 和 v₂ 之间，在表中表示为 E₁: v₁, v₂。

• 多边形表面表存储多边形中存在的表面数量。从下图可以看出，表面 S₁ 被边 E₁、E₂ 和 E₃ 覆盖，这些边可以在多边形表面表中表示为 S₁：E₁、E₂ 和 E₃。

平面方程

平面方程可以表示为 −

Ax + By + Cz + D = 0

其中 (x, y, z) 是平面上的任意一点，系数 A、B、C 和 D 是描述平面空间属性的常数。我们可以通过使用平面中三个非共线点的坐标值求解一组三个平面方程来获得 A、B、C 和 D 的值。假设平面的三个顶点分别为 (x₁、y₁、z₁)、(x₂、y₂、z₂) 和 (x₃、y₃、z₃)。

让我们求解以下比率 A/D、B/D 和 C/D 的联立方程。您将获得 A、B、C 和 D 的值。

(A/D) x₁ + (B/D) y₁ + （C/D）z₁ = -1

（A/D）x₂ + (B/D) y₂ + (C/D) z₂ = -1

（A/D）x₃ + (B/D) y₃ + (C/D) z₃ = -1

要以行列式形式获得上述方程，请将克莱姆规则应用于上述方程。

$A = \begin{bmatrix} 1& y_{1}& z_{1}\ 1& y_{2}& z_{2}\ 1& y_{3}& z_{3} \end{bmatrix} B = \begin{bmatrix} x_{1}& 1& z_{1}\ x_{2}& 1& z_{2}\ x_{3}& 1& z_{3} \end{bmatrix} C = \begin{bmatrix} x_{1}& y_{1}& 1\ x_{2}& y_{2}& 1\ x_{3}& y_{3}& 1 \end{bmatrix} D = - \begin{bmatrix} x_{1}& y_{1}& z_{1}\ x_{2}& y_{2}& z_{2}\ x_{3}& y_{3}& z_{3} \end{bmatrix}$

对于具有参数 A、B、C 和 D 的任何点 (x, y, z)，我们可以说 −

• Ax +By +Cz +D ≠ 0 表示该点不在平面上。

• Ax +By +Cz +D < 0 表示该点在表面内。

• Ax +By +Cz +D > 0 表示该点在表面外。

多边形网格

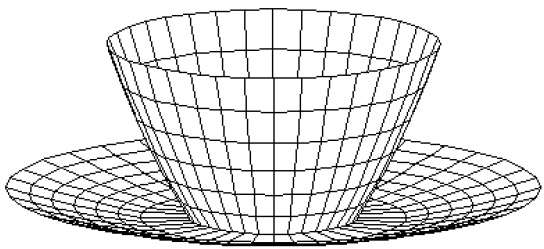
3D 表面和立体可以用一组多边形和线元素来近似。这样的表面称为多边形网格。在多边形网格中，每条边最多由两个多边形共享。多边形或面的集合共同构成了对象的"皮肤"。

此方法可用于表示图形中的一大类实体/表面。可以使用隐藏表面移除算法来渲染多边形网格。多边形网格可以用三种方式表示 −

• 显式表示
• 指向顶点列表的指针
• 指向边列表的指针

优点

• 它几乎可以用于建模任何对象。
• 它们很容易表示为顶点集合。
• 它们很容易转换。
• 它们很容易在计算机屏幕上绘制。

缺点

• 曲面只能近似描述。
• 很难模拟某些类型的物体，如头发或液体。