Heap Data Structure
Heap is a special case of balanced binary tree data structure where the root-node key is compared with its children and arranged accordingly. If α has child node β then −
key(α) ≥ key(β)
As the value of parent is greater than that of child, this property generates Max Heap. Based on this criteria, a heap can be of two types −
For Input → 35 33 42 10 14 19 27 44 26 31
Min-Heap − Where the value of the root node is less than or equal to either of its children.
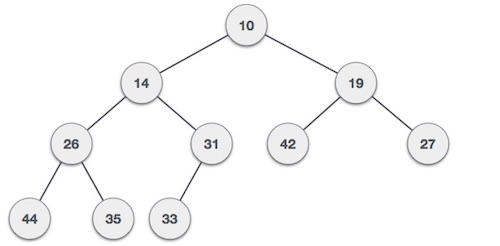
Max-Heap − Where the value of the root node is greater than or equal to either of its children.
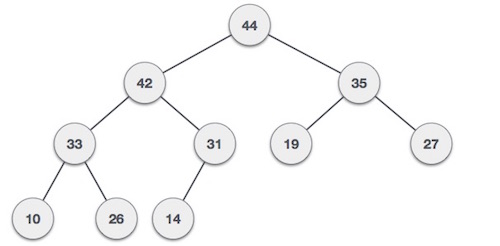
Both trees are constructed using the same input and order of arrival.
Max Heap Construction Algorithm
We shall use the same example to demonstrate how a Max Heap is created. The procedure to create Min Heap is similar but we go for min values instead of max values.
We are going to derive an algorithm for max heap by inserting one element at a time. At any point of time, heap must maintain its property. While insertion, we also assume that we are inserting a node in an already heapified tree.
Step 1 − Create a new node at the end of heap. Step 2 − Assign new value to the node. Step 3 − Compare the value of this child node with its parent. Step 4 − If value of parent is less than child, then swap them. Step 5 − Repeat step 3 & 4 until Heap property holds.
Note − In Min Heap construction algorithm, we expect the value of the parent node to be less than that of the child node.
Let's understand Max Heap construction by an animated illustration. We consider the same input sample that we used earlier.

Example
Following are the implementations of this operation in various programming languages −
//C code for Max Heap construction Algorithm
#include <stdio.h>
#include <stdlib.h>
// Structure to represent a heap
typedef struct {
int* array; // Array to store heap elements
int capacity; // Maximum capacity of the heap
int size; // Current size of the heap
} Heap;
// Function to create a new heap
Heap* createHeap(int capacity)
{
Heap* heap = (Heap*)malloc(sizeof(Heap));
heap->array = (int*)malloc(capacity * sizeof(int));
heap->capacity = capacity;
heap->size = 0;
return heap;
}
// Function to swap two elements in the heap
void swap(int* a, int* b)
{
int temp = *a;
*a = *b;
*b = temp;
}
// Function to heapify a subtree rooted at index i
void heapify(Heap* heap, int i)
{
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
// Check if the left child is larger than the root
if (left < heap->size && heap->array[left] > heap->array[largest])
largest = left;
// Check if the right child is larger than the largest so far
if (right < heap->size && heap->array[right] > heap->array[largest])
largest = right;
// If the largest is not the root, swap the root with the largest
if (largest != i) {
swap(&heap->array[i], &heap->array[largest]);
heapify(heap, largest);
}
}
// Function to insert a new element into the heap
void insert(Heap* heap, int value)
{
if (heap->size == heap->capacity) {
printf("Heap is full. Cannot insert more elements.
");
return;
}
// Insert the new element at the end
int i = heap->size++;
heap->array[i] = value;
// Fix the heap property if it is violated
while (i != 0 && heap->array[(i - 1) / 2] < heap->array[i]) {
swap(&heap->array[i], &heap->array[(i - 1) / 2]);
i = (i - 1) / 2;
}
}
// Function to extract the maximum element from the heap
int extractMax(Heap* heap)
{
if (heap->size == 0) {
printf("Heap is empty. Cannot extract maximum element.
");
return -1;
}
// Store the root element
int max = heap->array[0];
// Replace the root with the last element
heap->array[0] = heap->array[heap->size - 1];
heap->size--;
// Heapify the root
heapify(heap, 0);
return max;
}
// Function to print the elements of the heap
void printHeap(Heap* heap)
{
printf("Heap elements: ");
for (int i = 0; i < heap->size; i++) {
printf("%d ", heap->array[i]);
}
printf("
");
}
// Example usage of the heap
int main()
{
Heap* heap = createHeap(10);
insert(heap, 35);
insert(heap, 33);
insert(heap, 42);
insert(heap, 10);
insert(heap, 14);
insert(heap, 19);
insert(heap, 27);
insert(heap, 44);
insert(heap, 26);
insert(heap, 31);
printHeap(heap);
int max = extractMax(heap);
printf("Maximum element: %d
", max);
return 0;
}
Output
Heap elements: 44 42 35 33 31 19 27 10 26 14 Maximum element: 44
//C++ code for Max Heap construction Algorithm
#include <iostream>
// Structure to represent a heap
struct Heap {
int* array; // Array to store heap elements
int capacity; // Maximum capacity of the heap
int size; // Current size of the heap
};
// Function to create a new heap
Heap* createHeap(int capacity)
{
Heap* heap = new Heap;
heap->array = new int[capacity];
heap->capacity = capacity;
heap->size = 0;
return heap;
}
// Function to swap two elements in the heap
void swap(int& a, int& b)
{
int temp = a;
a = b;
b = temp;
}
// Function to heapify a subtree rooted at index i
void heapify(Heap* heap, int i)
{
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
// Check if the left child is larger than the root
if (left <heap->size && heap->array[left] > heap->array[largest])
largest = left;
// Check if the right child is larger than the largest so far
if (right <heap->size && heap->array[right] > heap->array[largest])
largest = right;
// If the largest is not the root, swap the root with the largest
if (largest != i) {
swap(heap->array[i], heap->array[largest]);
heapify(heap, largest);
}
}
// Function to insert a new element into the heap
void insert(Heap* heap, int value)
{
if (heap->size == heap->capacity) {
std::cout << "Heap is full. Cannot insert more elements." << std::endl;
return;
}
// Insert the new element at the end
int i = heap->size++;
heap->array[i] = value;
// Fix the heap property if it is violated
while (i != 0 && heap->array[(i - 1) / 2] < heap->array[i]) {
swap(heap->array[i], heap->array[(i - 1) / 2]);
i = (i - 1) / 2;
}
}
// Function to extract the maximum element from the heap
int extractMax(Heap* heap)
{
if (heap->size == 0) {
std::cout << "Heap is empty. Cannot extract maximum element." << std::endl;
return -1;
}
// Store the root element
int max = heap->array[0];
// Replace the root with the last element
heap->array[0] = heap->array[heap->size - 1];
heap->size--;
// Heapify the root
heapify(heap, 0);
return max;
}
// Function to print the elements of the heap
void printHeap(Heap* heap)
{
std::cout << "Heap elements: ";
for (int i = 0; i < heap->size; i++) {
std::cout << heap->array[i] << " ";
}
std::cout << std::endl;
}
// Example usage of the heap
int main()
{
Heap* heap = createHeap(10);
insert(heap, 35);
insert(heap, 33);
insert(heap, 42);
insert(heap, 10);
insert(heap, 14);
insert(heap, 19);
insert(heap, 27);
insert(heap, 44);
insert(heap, 26);
insert(heap, 31);
printHeap(heap);
int max = extractMax(heap);
std::cout << "Maximum element: " << max << std::endl;
return 0;
}
Output
Heap elements: 44 42 35 33 31 19 27 10 26 14 Maximum element: 44
// Java code for for Max Heap construction Algorithm
//Structure to represent a heap
public class MaxHeap {
private int[] heap; // To store heap elements
private int capacity; // Maximum capacity of the heap
private int size; // Current size of the heap
// To create a new heap
public MaxHeap(int capacity) {
this.capacity = capacity;
this.size = 0;
this.heap = new int[capacity];
}
private int parent(int i) {
return (i - 1) / 2;
}
private int leftChild(int i) {
return 2 * i + 1;
}
private int rightChild(int i) {
return 2 * i + 2;
}
private void swap(int i, int j) {
int temp = heap[i];
heap[i] = heap[j];
heap[j] = temp;
}
// Heapify a subtree rooted at index i
private void heapifyDown(int i) {
int largest = i;
int left = leftChild(i);
int right = rightChild(i);
// Check if the left child is larger than the root
if (left < size && heap[left] > heap[largest])
largest = left;
// Check if the right child is larger than the largest so far
if (right < size && heap[right] > heap[largest])
largest = right;
// If the largest is not the root, swap the root with the largest
if (largest != i) {
swap(i, largest);
heapifyDown(largest);
}
}
private void heapifyUp(int i) {
while (i > 0 && heap[i] > heap[parent(i)]) {
int parent = parent(i);
swap(i, parent);
i = parent;
}
}
// Insert the new element at the end
public void insert(int value) {
if (size == capacity) {
System.out.println("Heap is full. Cannot insert more elements.");
return;
}
heap[size] = value;
size++;
heapifyUp(size - 1);
}
// Function to extract the maximum element from the heap
public int extractMax() {
if (size == 0) {
System.out.println("Heap is empty. Cannot extract maximum element.");
return -1;
}
// store th root element
int max = heap[0];
//Replace the root with the last elements
heap[0] = heap[size - 1];
size--;
heapifyDown(0);
return max;
}
//print the elements of the heap
public void printHeap() {
System.out.print("Heap elements: ");
for (int i = 0; i < size; i++) {
System.out.print(heap[i] + " ");
}
System.out.println();
}
public static void main(String[] args) {
MaxHeap heap = new MaxHeap(10);
heap.insert(35);
heap.insert(33);
heap.insert(42);
heap.insert(10);
heap.insert(14);
heap.insert(19);
heap.insert(27);
heap.insert(44);
heap.insert(26);
heap.insert(31);
heap.printHeap();
int max = heap.extractMax();
System.out.println("Maximum element: " + max);
}
}
Output
Heap elements: 44 42 35 33 31 19 27 10 26 14 Maximum element: 44
# Python code for for Max Heap construction Algorithm
class MaxHeap:
def __init__(self):
self.heap = []
def parent(self, i):
return (i - 1) // 2
def left_child(self, i):
return 2 * i + 1
def right_child(self, i):
return 2 * i + 2
#Function to swap two elements in the heap
def swap(self, i, j):
self.heap[i], self.heap[j] = self.heap[j], self.heap[i]
# Function to heapify a subtree rooted at index i
def heapify_down(self, i):
left = self.left_child(i)
right = self.right_child(i)
largest = i
#Check if the left child is larger than the root
if left < len(self.heap) and self.heap[left] >self.heap[largest]:
largest = left
# Check if the right child is larger than the largest so far
if right < len(self.heap) and self.heap[right] > self.heap[largest]:
largest = right
# If the largest is not the root, swap the root with the largest
if largest != i:
self.swap(i, largest)
self.heapify_down(largest)
def heapify_up(self, i):
while i > 0 and self.heap[i] > self.heap[self.parent(i)]:
parent = self.parent(i)
self.swap(i, parent)
i = parent
# Insert the new element at the end
def insert(self, value):
self.heap.append(value)
# Fix the heap property if it is violated
self.heapify_up(len(self.heap) - 1)
# Function to extract the maximum element from the heap
def extract_max(self):
if len(self.heap) == 0:
print("Heap is empty. Cannot extract maximum element.")
return None
max_value = self.heap[0]
self.heap[0] = self.heap[-1]
self.heap.pop()
self.heapify_down(0)
return max_value
# Function to print the elements of the heap
def print_heap(self):
print("Heap elements:", end=" ")
for value in self.heap:
print(value, end=" ")
print()
# Example usage of the heap
heap = MaxHeap()
heap.insert(35)
heap.insert(33)
heap.insert(42)
heap.insert(10)
heap.insert(14)
heap.insert(19)
heap.insert(27)
heap.insert(44)
heap.insert(26)
heap.insert(31)
heap.print_heap()
max_value = heap.extract_max()
print("Maximum element:", max_value)
Output
Heap elements: 44 42 35 33 31 19 27 10 26 14 Maximum element: 44s
Max Heap Deletion Algorithm
Let us derive an algorithm to delete from max heap. Deletion in Max (or Min) Heap always happens at the root to remove the Maximum (or minimum) value.
Step 1 − Remove root node. Step 2 − Move the last element of last level to root. Step 3 − Compare the value of this child node with its parent. Step 4 − If value of parent is less than child, then swap them. Step 5 − Repeat step 3 & 4 until Heap property holds.
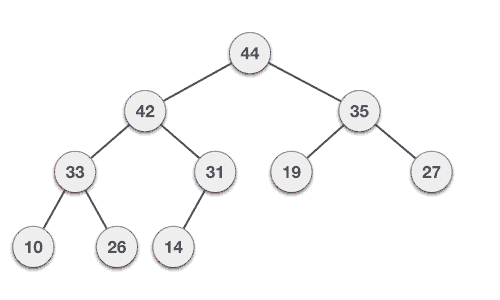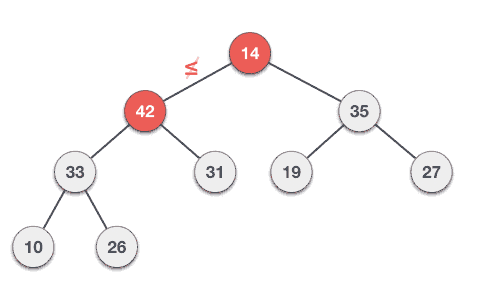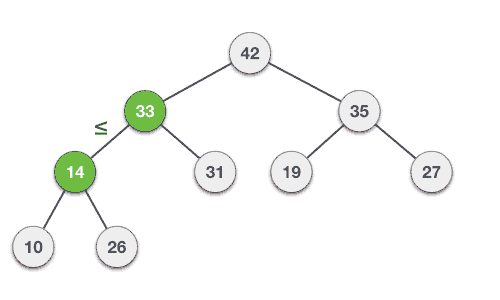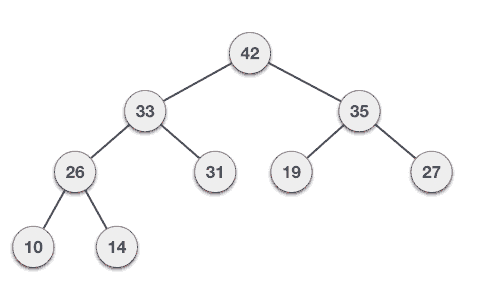
Example
Following are the implementations of this operation in various programming languages −
//C code for Max Heap Deletion Algorithm
#include <stdio.h>
#include <stdlib.h>
// Structure to represent a heap
typedef struct {
int* array; // Array to store heap elements
int capacity; // Maximum capacity of the heap
int size; // Current size of the heap
} Heap;
// create a new heap
Heap* createHeap(int capacity)
{
Heap* heap = (Heap*)malloc(sizeof(Heap));
heap->array = (int*)malloc(capacity * sizeof(int));
heap->capacity = capacity;
heap->size = 0;
return heap;
}
// swap two elements in the heap
void swap(int* a, int* b)
{
int temp = *a;
*a = *b;
*b = temp;
}
// Heapify a subtree rooted at index i
void heapify(Heap* heap, int i)
{
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
// Check if the left child is larger than the root
if (left < heap->size && heap->array[left] > heap->array[largest])
largest = left;
// Check if the right child is larger than the largest so far
if (right < heap->size && heap->array[right] > heap->array[largest])
largest = right;
// If the largest is not the root, swap the root with the largest
if (largest != i) {
swap(&heap->array[i], &heap->array[largest]);
heapify(heap, largest);
}
}
// Function to insert a new element into the heap
void insert(Heap* heap, int value)
{
if (heap->size == heap->capacity) {
printf("Heap is full. Cannot insert more elements.
");
return;
}
// Insert the new element at the end
int i = heap->size++;
heap->array[i] = value;
// Fix the heap property if it is violated
while (i != 0 && heap->array[(i - 1) / 2] < heap->array[i]) {
swap(&heap->array[i], &heap->array[(i - 1) / 2]);
i = (i - 1) / 2;
}
}
// delete the maximum element from the heap
int deleteMax(Heap* heap)
{
if (heap->size == 0) {
printf("Heap is empty. Cannot extract maximum element.
");
return -1;
}
// Store the root element
int max = heap->array[0];
// Replace the root with the last element
heap->array[0] = heap->array[heap->size - 1];
heap->size--;
// Heapify the root
heapify(heap, 0);
return max;
}
// print the elements of the heap
void printHeap(Heap* heap)
{
for (int i = 0; i < heap->size; i++) {
printf("%d ", heap->array[i]);
}
printf("
");
}
// Deallocate memory occupied by the heap
void destroyHeap(Heap* heap)
{
free(heap->array);
free(heap);
}
// Example usage of the heap
int main()
{
Heap* heap = createHeap(10);
insert(heap, 35);
insert(heap, 33);
insert(heap, 42);
insert(heap, 10);
insert(heap, 14);
insert(heap, 19);
insert(heap, 27);
insert(heap, 44);
insert(heap, 26);
insert(heap, 31);
printf("Heap elements before deletion: ");
printHeap(heap);
// Deleting the maximum element in the heap
int max = deleteMax(heap);
printf("Maximum element: %d
", max);
printf("Heap elements after deletion: ");
printHeap(heap);
destroyHeap(heap);
return 0;
}
Output
Heap elements before deletion: 44 42 35 33 31 19 27 10 26 14 Maximum element: 44 Heap elements after deletion: 42 33 35 26 31 19 27 10 14
//C++ code for Max Heap Deletion Algorithm
#include <iostream>
// Structure to represent a heap
struct Heap {
int* array; // Array to store heap elements
int capacity; // Maximum capacity of the heap
int size; // Current size of the heap
};
// Create a new heap
Heap* createHeap(int capacity)
{
Heap* heap = new Heap;
heap->array = new int[capacity];
heap->capacity = capacity;
heap->size = 0;
return heap;
}
// Swap two elements in the heap
void swap(int& a, int& b)
{
int temp = a;
a = b;
b = temp;
}
// Heapify a subtree rooted at index i
void heapify(Heap* heap, int i)
{
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
// Check if the left child is larger than the root
if (left < heap->size && heap->array[left] > heap->array[largest])
largest = left;
// Check if the right child is larger than the largest so far
if (right < heap->size && heap->array[right] > heap->array[largest])
largest = right;
// If the largest is not the root, swap the root with the largest
if (largest != i) {
swap(heap->array[i], heap->array[largest]);
heapify(heap, largest);
}
}
// Function to insert a new element into the heap
void insert(Heap* heap, int value)
{
if (heap->size == heap->capacity) {
std::cout << "Heap is full. Cannot insert more elements." << std::endl;
return;
}
// Insert the new element at the end
int i = heap->size++;
heap->array[i] = value;
// Fix the heap property if it is violated
while (i != 0 && heap->array[(i - 1) / 2] < heap->array[i]) {
swap(heap->array[i], heap->array[(i - 1) / 2]);
i = (i - 1) / 2;
}
}
// Function to delete the maximum element from the heap
int deleteMax(Heap* heap)
{
if (heap->size == 0) {
std::cout << "Heap is empty. Cannot extract maximum element." << std::endl;
return -1;
}
// Store the root element
int max = heap->array[0];
// Replace the root with the last element
heap->array[0] = heap->array[heap->size - 1];
heap->size--;
// Heapify the root
heapify(heap, 0);
return max;
}
// Function to print the elements of the heap
void printHeap(Heap* heap)
{
for (int i = 0; i < heap->size; i++) {
std::cout << heap->array[i] << " ";
}
std::cout << std::endl;
}
// Function to deallocate memory occupied by the heap
void destroyHeap(Heap* heap)
{
delete[] heap->array;
delete heap;
}
// Example usage of the heap
int main()
{
Heap* heap = createHeap(10);
insert(heap, 35);
insert(heap, 33);
insert(heap, 42);
insert(heap, 10);
insert(heap, 14);
insert(heap, 19);
insert(heap, 27);
insert(heap, 44);
insert(heap, 26);
insert(heap, 31);
std::cout << "Heap elements before deletion: ";
printHeap(heap);
int max = deleteMax(heap);
std::cout << "Maximum element: " << max << std::endl;
std::cout << "Heap elements after deletion: ";
printHeap(heap);
destroyHeap(heap);
return 0;
}
Output
Heap elements before deletion: 44 42 35 33 31 19 27 10 26 14 Maximum element: 44 Heap elements after deletion: 42 33 35 26 31 19 27 10 14
// Java code for for Max Heap Deletion Algorithm
// Structure to represent a heap
class Heap {
private int[] array; // Array to store heap elements
private int capacity; // Maximum capacity of the heap
private int size; // Current size of the heap
// To create a new heap
public Heap(int capacity) {
this.array = new int[capacity];
this.capacity = capacity;
this.size = 0;
}
// Swap two elements in the heap
private void swap(int a, int b) {
int temp = array[a];
array[a] = array[b];
array[b] = temp;
}
// Heapify a subtree rooted at index i
private void heapify(int i) {
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
// Check if the left child is larger than the root
if (left < size && array[left] > array[largest])
largest = left;
// Check if the right child is larger than the largest so far
if (right < size && array[right] > array[largest])
largest = right;
// If the largest is not the root, swap the root with the largest
if (largest != i) {
swap(i, largest);
heapify(largest);
}
}
// Insert a new element into the heap
public void insert(int value) {
if (size == capacity) {
System.out.println("Heap is full. Cannot insert more elements.");
return;
}
// Insert the new element at the end
int i = size++;
array[i] = value;
// Fix the heap property if it is violated
while (i != 0 && array[(i - 1) / 2] < array[i]) {
swap(i, (i - 1) / 2);
i = (i - 1) / 2;
}
}
// Delete the maximum element from the heap
public int deleteMax() {
if (size == 0) {
System.out.println("Heap is empty. Cannot extract maximum element.");
return -1;
}
// Store the root element
int max = array[0];
// Replace the root with the last element
array[0] = array[size - 1];
size--;
// Heapify the root
heapify(0);
return max;
}
// Print the elements of the heap
public void printHeap() {
for (int i = 0; i < size; i++) {
System.out.print(array[i] + " ");
}
System.out.println();
}
// Deallocate memory occupied by the heap
public void destroyHeap() {
array = null;
size = 0;
}
}
//Inserting the elements
public class Main {
public static void main(String[] args) {
Heap heap = new Heap(10);
heap.insert(35);
heap.insert(33);
heap.insert(42);
heap.insert(10);
heap.insert(14);
heap.insert(19);
heap.insert(27);
heap.insert(44);
heap.insert(26);
heap.insert(31);
System.out.print("Heap elements before deletion: ");
heap.printHeap();
int max = heap.deleteMax();
System.out.println("Maximum element: " + max);
//Printing the heap elements after deletion of max element
System.out.print("Heap elements after deletion: ");
heap.printHeap();
heap.destroyHeap();
}
}
Output
Heap elements before deletion: 44 42 35 33 31 19 27 10 26 14 Maximum element: 44 Heap elements after deletion: 42 33 35 26 31 19 27 10 14
#Python code for Max Heap Deletion Algorithm
class Heap:
def __init__(self, capacity):
self.array = [0] * capacity #array to store heap elements
self.capacity = capacity #maximum capacity of the heap
self.size = 0 #Current size of the heap
# swap two elements in the heap
def swap(self, a, b):
self.array[a], self.array[b] = self.array[b], self.array[a]
# Heapify a subtree rooted at index i
def heapify(self, i):
largest = i
left = 2 * i + 1
right = 2 * i + 2
# Check if the left child is larger than the root
if left < self.size and self.array[left] > self.array[largest]:
largest = left
# Check if the right child is larger than the largest so far
if right < self.size and self.array[right] > self.array[largest]:
largest = right
# If the largest is not the root, swap the root with the largest
if largest != i:
self.swap(i, largest)
self.heapify(largest)
# insert a new element into the heap
def insert(self, value):
if self.size == self.capacity:
print("Heap is full. Cannot insert more elements.")
return
# Insert the new element at the end
i = self.size
self.size += 1
self.array[i] = value
# Fix the heap property if it is violated
while i != 0 and self.array[(i - 1) // 2] < self.array[i]:
self.swap(i, (i - 1) // 2)
i = (i - 1) // 2
# delete the maximum element from the heap
def deleteMax(self):
if self.size == 0:
print("Heap is empty. Cannot extract maximum element.")
return -1
# store the root element
max_value = self.array[0]
# Replace the root with the last element
self.array[0] = self.array[self.size - 1]
self.size -= 1
# Heapify the root
self.heapify(0)
return max_value
# print the elements of the heap
def printHeap(self):
for i in range(self.size):
print(self.array[i], end=" ")
print()
# deallocate memory occupied by the heap
def destroyHeap(self):
self.array = []
self.size = 0
# Example usage of the heap
heap = Heap(10)
heap.insert(35)
heap.insert(33)
heap.insert(42)
heap.insert(10)
heap.insert(14)
heap.insert(19)
heap.insert(27)
heap.insert(44)
heap.insert(26)
heap.insert(31)
print("Heap elements before deletion:", end=" ")
heap.printHeap()
max_value = heap.deleteMax()
print("Maximum element:", max_value)
print("Heap elements after deletion:", end=" ")
heap.printHeap()
heap.destroyHeap()
Output
Heap elements before deletion: 44 42 35 33 31 19 27 10 26 14 Maximum element: 44 Heap elements after deletion: 42 33 35 26 31 19 27 10 14



