对数放大器和反对数放大器

执行数学运算(如对数和反对数(指数))并带有放大功能的电子电路分别称为对数放大器和反对数放大器。

本章详细讨论了对数放大器和反对数放大器。请注意，这些放大器属于非线性应用。

对数放大器

对数放大器或对数放大器是一种电子电路，其产生的输出与所施加输入的对数成比例。本节详细讨论了基于运算放大器的对数放大器。

基于运算放大器的对数放大器在输出端产生一个电压，该电压与施加到连接到其反相端的电阻上的电压的对数成比例。基于运算放大器的对数放大器的电路图如下图所示 −

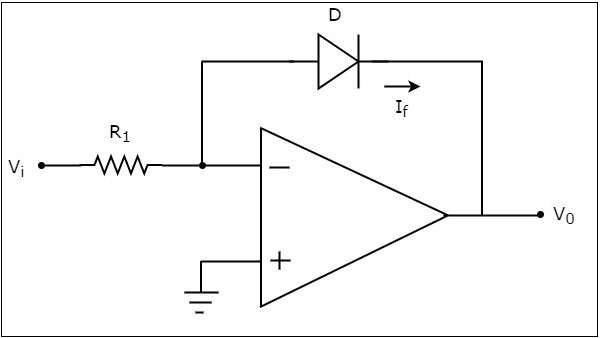
在上述电路中，运算放大器的非反相输入端接地。这意味着在运算放大器的非反相输入端施加零伏电压。

根据虚拟短路概念，运算放大器的反相输入端的电压将等于其非反相输入端的电压。因此，反相输入端的电压将为零伏。

反相输入端节点的节点方程为 −

$$\frac{0-V_i}{R_1}+I_{f}=0$$

$$=>I_{f}=\frac{V_i}{R_1}......公式 1$$

以下是当二极管处于正向偏置时，流过二极管的电流的方程 −

$$I_{f}=I_{s} e^{(\frac{V_f}{nV_T})} ......公式 2$$

其中，

$I_{s}$ 是二极管的饱和电流二极管，

$V_{f}$ 是二极管正向偏置时的压降，

$V_{T}$ 是二极管的热等效电压。

运算放大器反馈环路周围的 KVL 方程 将是 −

$$0-V_{f}-V_{0}=0$$

$$=>V_{f}=-V_{0}$$

将 $V_{f}$ 的值代入公式 2 中，我们得到 −

$$I_{f}=I_{s} e^{\left(\frac{-V_0}{nV_T} ight)} ......公式 3$$

注意公式 1 的左侧项和方程 3 相同。因此，将这两个方程的右边项相等，如下所示 −

$$\frac{V_i}{R_1}=I_{s}e^{\left(\frac{-V_0}{nV_T} ight)}$$

$$\frac{V_i}{R_1I_s}= e^{\left(\frac{-V_0}{nV_T} ight)}$$

在两边应用自然对数，我们得到 −

$$In\left(\frac{V_i}{R_1I_s} ight)= \frac{-V_0}{nV_T}$$

$$V_{0}=-{nV_T}In\left(\frac{V_i}{R_1I_s} ight)$$

请注意，在上面的等式中，参数 n、${V_T}$ 和 $I_{s}$ 是常数。因此，对于固定电阻值 $R_{1}$，输出电压 $V_{0}$ 将与输入电压 $V_{i}$ 的自然对数成比例。

因此，当 ${R_1I_s}=1V$ 时，上述基于运算放大器的对数放大器电路将产生与输入电压 ${V_T}$ 的自然对数成比例的输出。

观察到输出电压 $V_{0}$ 具有负号，这表明输入和输出之间存在 180⁰ 的相位差。

反对数放大器

反对数放大器或反对数放大器是一种产生与输入电压 $V_T}$ 的自然对数成比例的输出的电子电路与施加输入的反对数成正比。本节详细讨论了基于运算放大器的反对数放大器。

基于运算放大器的反对数放大器在输出端产生一个电压，该电压与施加到连接到其反相端的二极管上的电压的反对数成正比。

基于运算放大器的反对数放大器的电路图如下图所示 −

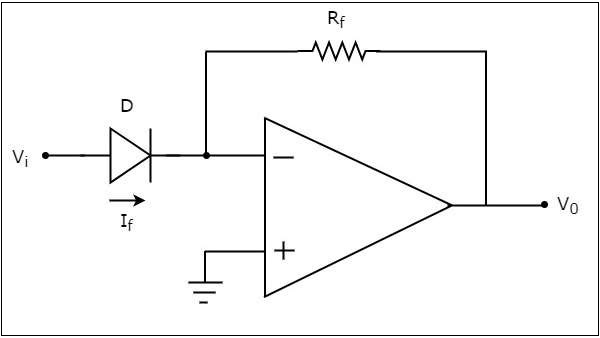
在上图所示的电路中，运算放大器的非反相输入端接地。这意味着在其非反相输入端施加零伏电压。

根据虚拟短路概念，运算放大器反相输入端的电压将等于其非反相输入端的电压。因此，其反相输入端的电压将为零伏。

反相输入端节点的节点方程为 −

$$-I_{f}+\frac{0-V_0}{R_f}=0$$

$$=>-\frac{V_0}{R_f}=I_{f}$$

$$=>V_{0}=-R_{f}I_{f}.........公式 4$$

我们知道，当二极管处于正向偏置时，流过二极管的电流方程如下所示 −

$$I_{f}=I_{s} e^{\left(\frac{V_f}{nV_T} ight)}$$

代入值公式 4 中的 $I_{f}$，我们得到

$$V_{0}=-R_{f}\left \{{I_{s} e^{\left(\frac{V_f}{nV_T} ight)}} ight \}$$

$$V_{0}=-R_{f}{I_{s} e^{\left(\frac{V_f}{nV_T} ight)}}......公式 5$$

运算放大器反相端输入侧的 KVL 方程为

$$V_{i}-V_{f}=0$$

$$V_{f}=V_{i}$$

代入公式 5 中的 𝑉𝑓 值，我们得到−

$$V_{0}=-R_{f}{I_{s} e^{\left(\frac{V_i}{nV_T} ight)}}$$

请注意，在上面的等式中，参数 n、${V_T}$ 和 $I_{s}$ 是常数。因此，对于固定的反馈电阻 ${R_f}$，输出电压 ${V_0}$ 将与输入电压 ${V_i}$ 的反对数(指数)成正比。

因此，当 ${R_fI_s}= 1V$ 时，上面讨论的基于运算放大器的反对数放大器电路将产生一个输出，该输出与输入电压 ${V_i}$ 的反对数(指数)成正比。观察到输出电压 ${V_0}$ 具有负号，这表明输入和输出之间存在 180⁰ 的相位差。