Plotly - 极坐标图和雷达图

在本章中，我们将学习如何借助 Plotly 制作极坐标图和雷达图。

首先，让我们学习一下极坐标图。

极坐标图

极坐标图是圆形图的常见变体。当数据点之间的关系可以最容易地以半径和角度的形式可视化时，它很有用。

在极坐标图中，一系列数据由连接极坐标系中点的闭合曲线表示。每个数据点由与极点的距离（径向坐标）和与固定方向的角度（角坐标）决定。

极坐标图表示沿径向和角轴的数据。径向和角坐标由 go.Scatterpolar() 函数的 r 和 theta 参数给出。西塔数据可以是分类数据，但数值数据也是可能的，并且是最常用的数据。

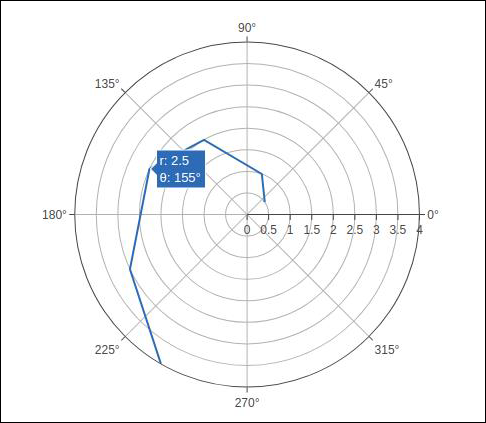
以下代码生成一个基本的极坐标图。除了 r 和 theta 参数外，我们还将模式设置为 lines（也可以将其设置为 markers，在这种情况下只会显示数据点）。

import numpy as np
r1 = [0,6,12,18,24,30,36,42,48,54,60]
t1 = [1,0.995,0.978,0.951,0.914,0.866,0.809,0.743,0.669,0.588,0.5]
trace = go.Scatterpolar(
   r = [0.5,1,2,2.5,3,4],
   theta = [35,70,120,155,205,240],
   mode = 'lines',
)
data = [trace]
fig = go.Figure(data = data)
iplot(fig)

输出结果如下所示 −

以下示例中，来自 逗号分隔值 (CSV) 文件 的数据用于生成极坐标图。polar.csv 的前几行如下所示 −

y,x1,x2,x3,x4,x5,
0,1,1,1,1,1,
6,0.995,0.997,0.996,0.998,0.997,
12,0.978,0.989,0.984,0.993,0.986,
18,0.951,0.976,0.963,0.985,0.969,
24,0.914,0.957,0.935,0.974,0.946,
30,0.866,0.933,0.9,0.96,0.916,
36,0.809,0.905,0.857,0.943,0.88,
42,0.743,0.872,0.807,0.923,0.838,
48,0.669,0.835,0.752,0.901,0.792,
54,0.588,0.794,0.691,0.876,0.74,
60,0.5,0.75,0.625,0.85,0.685,

在笔记本的输入单元中输入以下脚本以生成极坐标图，如下所示 −

import pandas as pd
df = pd.read_csv("polar.csv")
t1 = go.Scatterpolar(
   r = df['x1'], theta = df['y'], mode = 'lines', name = 't1'
)
t2 = go.Scatterpolar(
   r = df['x2'], theta = df['y'], mode = 'lines', name = 't2'
)
t3 = go.Scatterpolar(
   r = df['x3'], theta = df['y'], mode = 'lines', name = 't3'
)
data = [t1,t2,t3]
fig = go.Figure(data = data)
iplot(fig)

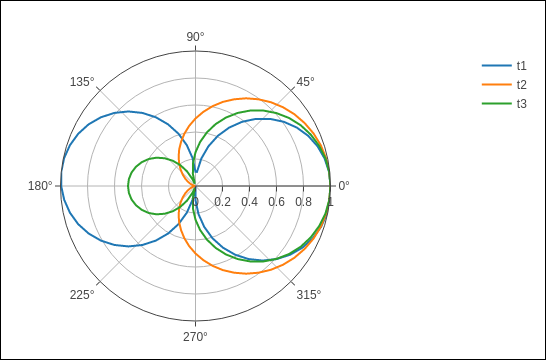
下面给出了上述代码的输出 −

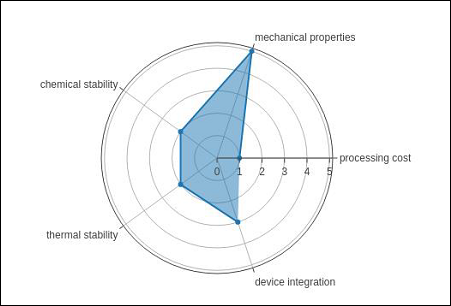
雷达图

雷达图（也称为蜘蛛图或星形图）以二维图表的形式显示多变量数据，这些定量变量以中心为起点，以轴为单位表示。轴的相对位置和角度通常不具参考价值。

对于雷达图，一般情况下，在go.Scatterpolar()函数中使用带有分类角度变量的极坐标图。

以下代码使用Scatterpolar()函数呈现基本雷达图 −

radar = go.Scatterpolar(
   r = [1, 5, 2, 2, 3],
   theta = [
      'processing cost',
      'mechanical properties',
      'chemical stability', 
      'thermal stability',
      'device integration'
   ],
   fill = 'toself'
)
data = [radar]
fig = go.Figure(data = data)
iplot(fig)

下面提到的输出是上面给出的代码的结果 −