图论 - 树
树是甚至不包含单个循环的图。它们以图形形式表示层次结构。树属于最简单的图类。尽管它们很简单,但它们具有丰富的结构。
树提供了一系列有用的应用,从简单的家谱到复杂的计算机科学数据结构中的树。
树
连通无环图称为树。换句话说,没有循环的连通图称为树。
树的边称为分支。树的元素称为其节点。没有子节点的节点称为叶节点。
具有"n"个顶点的树具有"n-1"条边。如果它比'n-1'多了一个边,那么这个额外的边显然必须与两个顶点配对,从而形成一个循环。然后,它就变成了一个循环图,这违反了树图。
示例 1
此处显示的图是一棵树,因为它没有循环并且是连通的。它有四个顶点和三个边,即对于'n'个顶点,有'n-1'条边,如定义中所述。
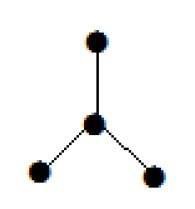
注意 −每棵树至少有两个度为 1 的顶点。
示例 2
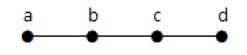
在上面的例子中,顶点"a"和"d"的度为 1。而另外两个顶点"b"和"c"的度为 2。这是可能的,因为为了不形成循环,图中的任何地方都应该至少有两个单边。它只不过是两个度为 1 的边。
森林
不连通的无环图称为森林。换句话说,不相交的树集合称为森林。
示例
下图看起来像两个子图;但它是一个单独的不连通图。此图中没有循环。因此,显然它是一片森林。
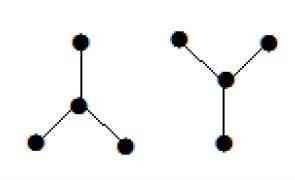
生成树
设 G 为连通图,则 G 的子图 H 称为 G 的生成树,如果 −
- H 是一棵树
- H 包含 G 的所有顶点。
无向图 G 的生成树 T 是包含 G 所有顶点的子图。
示例
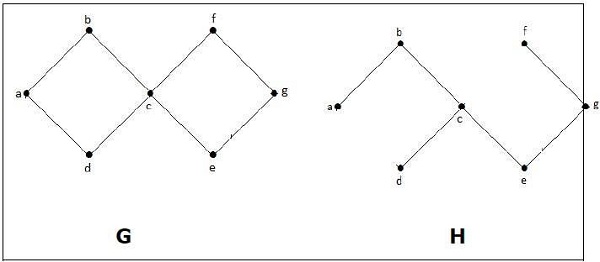
在上面的例子中,G 是一个连通图,H 是 G 的一个子图。
显然,图 H 没有循环,它是一棵有六条边的树,比顶点总数少一条。因此,H 是 G 的生成树。
电路等级
假设"G"是一个有"n"个顶点和"m"条边的连通图。G 的生成树"T"包含 (n-1) 条边。
因此,为了得到生成树,您需要从"G"中删除的边数 = m-(n-1),这称为 G 的电路等级。
这个公式是正确的,因为在生成树中您需要有"n-1"条边。在'm'条边中,您需要在图中保留'n-1'条边。
因此,从'm'中删除'n-1'条边会从图中移除这些边,从而得到一棵不应形成循环的生成树。
示例
查看以下图表 −
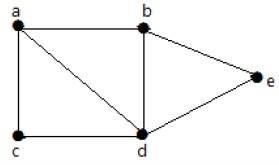
对于上例中的图,有 m=7 条边和 n=5 个顶点。
那么电路等级为 −
示例
假设"G"是一个有六个顶点的连通图,每个顶点的度为 3。求"G"的电路秩。
根据顶点度和定理,
基尔霍夫定理
基尔霍夫定理有助于确定连通图可以形成的生成树的数量。
示例
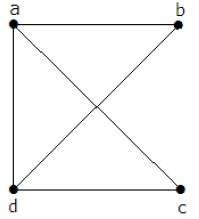
矩阵"A"应填充为,如果两个顶点之间有一条边,则应将其赋为"1",否则应赋为"0"。
$$A=\begin{vmatrix}0 & a & b & c & d\a & 0 & 1 & 1 & 1 \b & 1 & 0 & 0 & 1\c & 1 & 0 & 0 & 1\d & 1 & 1 & 1 & 0 \end{vmatrix} = \begin{vmatrix} 0 & 1 & 1 & 1\1 & 0 & 0 & 1\1 & 0 & 0 & 1\1 & 1 & 1 & 0\end{vmatrix}$$利用基尔霍夫定理,应将其改为用顶点的度数代替主对角线值,其他所有元素都用 -1.A
$$=\begin{vmatrix} 3 & -1 & -1 & -1\-1 & 2 & 0 & -1\-1 & 0 & 2 & -1\-1 & -1 & -1 & 3 \end{vmatrix}=M$$ $$M=\begin{vmatrix}3 & -1 & -1 & -1\-1 & 2 & 0 & -1\-1 & 0 & 2 & -1\-1 & -1 & -1 & 3 \end{vmatrix} =8$$ $$Co\:\:factor\:\:of\:\:m1\:\:= \begin{vmatrix} 2 & 0 & -1\0 & 2 & -1\-1 & -1 & 3\end{vmatrix}$$因此,生成树的数量 = 8。


