图论 - 可遍历性

如果可以在所有顶点之间绘制一条路径而不需要重新追踪同一路径，则该图是可遍历的。 基于这条路径，本章描述了一些类别，例如欧拉路径和欧拉回路。

欧拉路径

欧拉路径包含"G"的每条边恰好一次，并且"G"的每个顶点至少包含一次。 如果连通图 G 包含欧拉路径，则称其是可遍历的。

示例

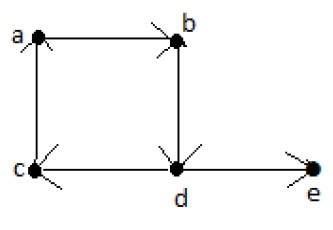
欧拉路径 = d-c-a-b-d-e。

欧拉电路

在欧拉路径中，如果起始顶点与其结束顶点相同，则称为欧拉回路。

示例

欧拉路径 = a-b-c-d-a-g-f-e-c-a。

欧拉电路定理

连通图 G 是可遍历的当且仅当 G 中奇数度的顶点数量恰好为 2 或 0。 如果连通图 G 恰好有两个度数为奇数的顶点，则它可以包含欧拉路径，但不能包含欧拉回路。

注意 − 该欧拉路径以一个奇数度的顶点开始，以另一个奇数度的顶点结束。

示例

欧拉路径 − b-e-a-b-d-c-a 不是欧拉回路，但它是欧拉路径。 显然它有 2 个奇数度顶点。

注意 − 在连通图G中，如果奇数度的顶点数=0，则欧拉回路存在。

哈密尔顿图

如果存在包含 G 的所有顶点的环，则称连通图 G 为哈密顿图。

每个周期都是一个电路，但一个电路可以包含多个周期。 这样的循环称为 G 的哈密尔顿循环。

哈密尔顿路径

如果连通图仅包含 G 的每个顶点一次，则该连通图被称为哈密顿图。 这样的路径称为哈密尔顿路径。

示例

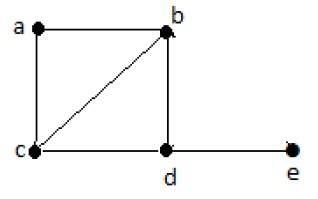
哈密尔顿路径− e-d-b-a-c。

注意

• 欧拉电路只包含图的每条边一次。

• 在哈密顿循环中，可以跳过图的某些边。

示例

看看下面的图表−

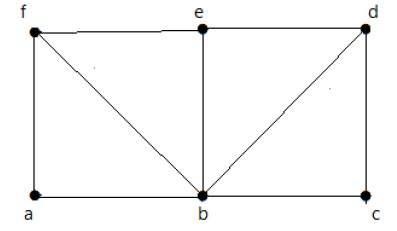
对于上图所示 −

• 欧拉路径存在 - false

• 欧拉回路存在 - false

• 哈密尔顿循环存在 - true

• 哈密尔顿路径存在 - true

G 有四个奇数度的顶点，因此它不可遍历。 通过跳过内部边，该图具有穿过所有顶点的哈密顿循环。