图论 - 基础知识
图是点和与点相连的线的示意图。它至少有一条线连接一组两个顶点,但没有顶点连接自身。图论中的图概念基于一些基本术语,例如点、线、顶点、边、顶点度、图的属性等。在本章中,我们将介绍图论的这些基础知识。
点
点是一维、二维或三维空间中的特定位置。为了更好地理解,可以用字母表示点。它可以用一个点来表示。
示例
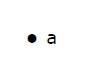
此处,点是名为"a"的点。
线
线是两点之间的连接。它可以用实线表示。
示例

此处,"a"和"b"是点。这两点之间的链接称为线。
顶点
顶点是多条线相交的点。它也被称为节点。与点类似,顶点也用字母表示。
示例

此处,顶点用字母"a"命名。
边
边是连接两个顶点的线的数学术语。一个顶点可以形成多条边。没有顶点,就无法形成边。边必须有一个起始顶点和一个终止顶点。
示例

这里,"a"和"b"是两个顶点,它们之间的链接称为边。
图
图"G"定义为 G = (V, E),其中 V 是图中所有顶点的集合,E 是图中所有边的集合。
示例 1
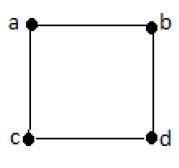
在上面的例子中,ab、ac、cd 和 bd 是图的边。类似地,a、b、c 和 d 是图的顶点。
示例 2
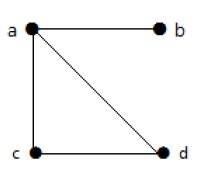
此图中有四个顶点 a、b、c 和 d,以及四条边 ab、ac、ad 和 cd。
循环
在图中,如果从顶点到自身绘制一条边,则称为循环。
示例 1

在上图中,V 是一个顶点,它有一条边 (V, V) 形成一个循环。
示例2

在此图中,有两个循环,分别在顶点 a 和顶点 b 处形成。
顶点的度
它是与顶点 V 相邻的顶点数。
符号 − deg(V)。
在具有 n 个顶点的简单图中,任何顶点的度为 −
deg(v) ≤ n – 1 ∀ v ∈ G
顶点可以与除自身之外的所有其他顶点形成边。因此顶点的度将达到图中顶点数减 1。这个 1 是针对自顶点的,因为它本身不能形成环路。如果任何一个顶点都有环路,那么它就不是简单图。
顶点的度可以在两种图情况下考虑 −
无向图
有向图
无向图中顶点的度
无向图没有有向边。请考虑以下示例。
示例 1
查看以下图表 −
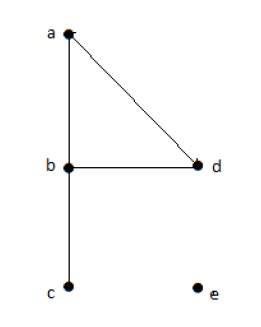
在上述无向图中,
deg(a) = 2,因为在顶点'a'处有 2 条边相交。
deg(b) = 3,因为在顶点'b'处有 3 条边相交。
deg(c) = 1,因为在顶点'c'处形成 1 条边
因此'c'是悬垂顶点。
deg(d) = 2,因为有 2 条边在顶点'd'处相交。
deg(e) = 0,因为在顶点'e'处形成 0 条边。
因此'e'是一个孤立顶点。
示例 2
查看以下图表 −
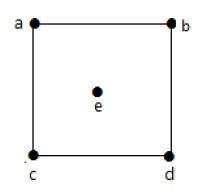
在上图中,
deg(a) = 2、deg(b) = 2、deg(c) = 2、deg(d) = 2 和 deg(e) = 0。
顶点"e"是一个孤立顶点。该图没有任何悬垂顶点。
有向图中的顶点度
在有向图中,每个顶点都有一个入度和一个出度。
图的入度
顶点 V 的入度是进入顶点 V 的边的数量。
符号 − deg−(V)。
图的出度
顶点 V 的出度是从顶点 V 出去的边的数量。
符号 − deg+(V)。
考虑以下示例。
示例 1
查看以下有向图。顶点"a"有两条边"ad"和"ab",它们向外延伸。因此它的出度为 2。同样,有一条边"ga",朝向顶点"a"。因此"a"的入度为 1。
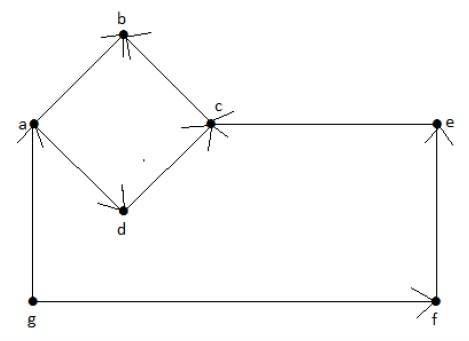
其他顶点的入度和出度如下表所示 −
| 顶点 | 入度 | 出度 |
|---|---|---|
| a | 1 | 2 |
| b | 2 | 0 |
| c | 2 | 1 |
| d | 1 | 1 |
| e | 1 | 1 |
| f | 1 | 1 |
| g | 0 | 2 |
示例 2
查看以下有向图。顶点"a"具有从顶点"a"向外延伸的边"ae"。因此其出度为 1。类似地,该图具有朝向顶点"a"的边"ba"。因此"a"的入度为 1。
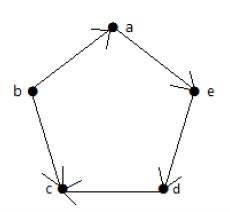
其他顶点的入度和出度如下表所示 −
| 顶点 | 入度 | 出度 |
|---|---|---|
| a | 1 | 1 |
| b | 0 | 2 |
| c | 2 | 0 |
| d | 1 | 1 |
| e | 1 | 1 |
悬垂顶点
通过使用顶点的度数,我们有两种特殊类型的顶点。度数为 1 的顶点称为悬垂顶点。
示例

在此示例中,顶点"a"和顶点"b"具有连通边"ab"。因此,对于顶点"a",只有一条指向顶点"b"的边,同样,对于顶点"b",只有一条指向顶点"a"的边。最后,顶点"a"和顶点"b"的度为 1,也称为悬垂顶点。
孤立顶点
度为零的顶点称为孤立顶点。
示例

此处,顶点"a"和顶点"b"彼此之间以及与任何其他顶点之间没有连通性。因此顶点"a"和"b"的度均为零。这些也被称为孤立顶点。
邻接
以下是邻接的范式 −
在图中,如果两个顶点之间有一条边,则称这两个顶点相邻。此处,顶点的邻接由连接这两个顶点的单个边维持。
在图中,如果两个边之间有一个公共顶点,则称这两个边相邻。此处,边的邻接由连接两个边的单个顶点维持。
示例 1
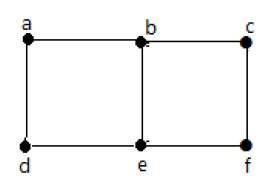
在上图中 −
'a' 和 'b' 是相邻顶点,因为它们之间有一条共同边 'ab'。
'a' 和 'd' 是相邻顶点,因为它们之间有一条共同边 'ad'。
'ab' 和 'be' 是相邻边,因为它们之间有一条共同顶点 'b'。
'be' 和 'de' 是相邻边,因为它们之间有一条共同顶点 'e'。
示例 2
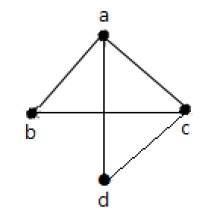
在上图中−
'a' 和 'd' 是相邻顶点,因为它们之间有共同边 'ad'。
'c' 和 'b' 是相邻顶点,因为它们之间有共同边 'cb'。
'ad' 和 'cd' 是相邻边,因为它们之间有共同顶点 'd'。
'ac' 和 'cd' 是相邻边,因为它们之间有共同顶点 'c'。
平行边
在图中,如果一对顶点由多条边连接,则这些边称为平行边。
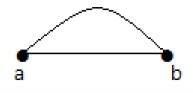
在上图中,"a"和"b"是两个顶点,它们之间由两条边"ab"和"ab"连接。因此,它被称为平行边。
多图
具有平行边的图称为多图。
示例 1
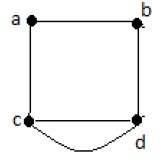
在上图中,有五条边"ab"、"ac"、"cd"、"cd"和"bd"。由于"c"和"d"之间有两条平行边,因此它是一个多重图。
示例 2
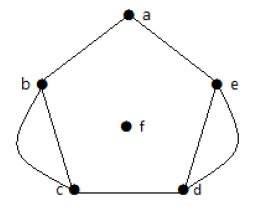
在上图中,顶点"b"和"c"有两条边。顶点"e"和"d"之间也有两条边。因此它是一个多重图。
图的度序列
如果图中所有顶点的度按降序或升序排列,则获得的序列称为图的度序列。
示例 1
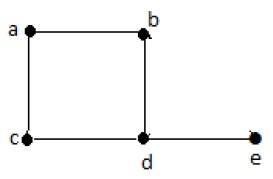
| 顶点 | A | b | c | d | e |
|---|---|---|---|---|---|
| 连接到 | b,c | a,d | a,d | c,b,e | d |
| 度 | 2 | 2 | 2 | 3 | 1 |
在上图中,对于顶点 {d, a, b, c, e},度序列为 {3, 2, 2, 2, 1}。
示例 2
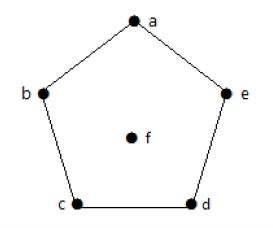
| 顶点 | A | b | c | d | e | f |
|---|---|---|---|---|---|---|
| 连接到 | b,e | a,c | b,d | c,e | a,d | - |
| 度 | 2 | 2 | 2 | 2 | 0 |
在上面图中,对于顶点 {a, b, c, d, e, f},度序列为 {2, 2, 2, 2, 2, 0}。


