图论 - 连通性
是否可以从一个顶点遍历图到另一个顶点取决于图的连接方式。连通性是图论中的一个基本概念。连通性定义图是连通的还是断开的。它有基于边和顶点的子主题,称为边连通性和顶点连通性。让我们详细讨论它们。
连通性
如果每对顶点之间都有一条路径,则称图为连通。从每个顶点到任何其他顶点,都应该有一些路径可以遍历。这称为图的连通性。具有多个断开的顶点和边的图被称为断开的。
示例 1
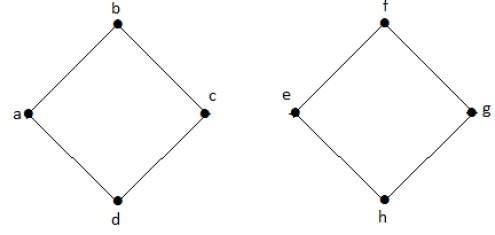
在下图中,可以从一个顶点移动到任何其他顶点。例如,可以使用路径"a-b-e"从顶点"a"遍历到顶点"e"。
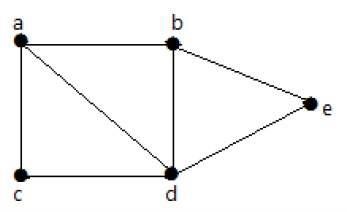
示例 2
在下面的例子中,从顶点"a"遍历到顶点"f"是不可能的,因为它们之间没有直接或间接的路径。因此它是一个断开的图。
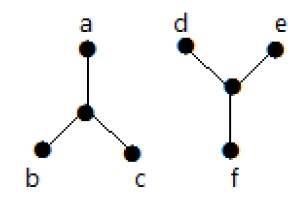
切断顶点
让"G"成为一个连通图。如果"G-V"(从"G"中删除"V")导致断开的图,则顶点 V ∈ G 称为"G"的切断顶点。从图中删除一个割顶点会将其拆分为两个或更多个图。
注意 − 删除一个割顶点可能会导致图断开连接。
连通图"G"最多可以有 (n-2) 个割顶点。
示例
在下图中,顶点"e"和"c"是割顶点。
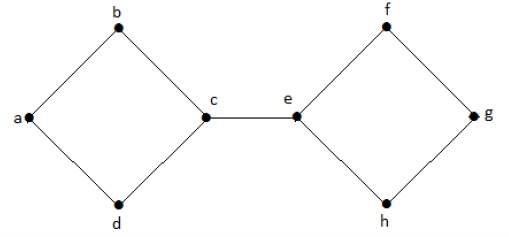
通过删除"e"或"c",图将变为断开连接的图。

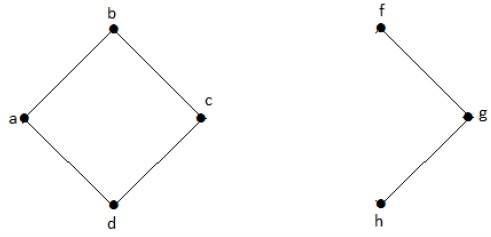
如果没有'g',顶点'c'和顶点'h'以及其他许多顶点之间就没有路径。因此,它是一个断开图,切点为'e'。同样,'c'也是上述图的切点。
切边(桥)
让'G'成为一个连通图。边'e' ∈如果"G-e"导致图断开,则 G 称为割边。
如果移除图中的一条边会导致两个或多个图,则该边称为割边。
示例
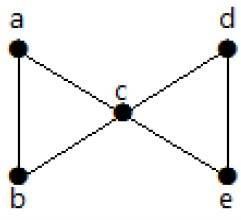
在下图中,割边为 [(c, e)]。

通过从图中移除边 (c, e),它变为断开的图。

在上图中,移除边 (c, e) 会将图分成两个,即只不过是一个不连通的图。因此,边 (c, e) 是图的一条割边。
注意 − 假设"G"是一个有"n"个顶点的连通图,那么
当且仅当边"e"不是 G 中任何循环的一部分时,割边 e ∈ G。
可能的最大割边数为"n-1"。
只要存在割边,割顶点也存在,因为割边的至少一个顶点是割顶点。
如果存在割顶点,则割边可能存在也可能不存在。
图的割集
设"G"= (V, E) 为连通图。如果从 G 中删除 E' 的所有边会导致 G 断开,则 E 的子集 E' 称为 G 的割集。
如果从图中删除一定数量的边会导致图断开,则这些被删除的边称为图的割集。
示例
请看下图。其割集为 E1 = {e1, e3, e5, e8}。
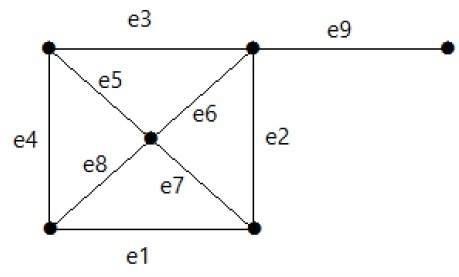
从图中删除割集 E1 后,将如下所示 −
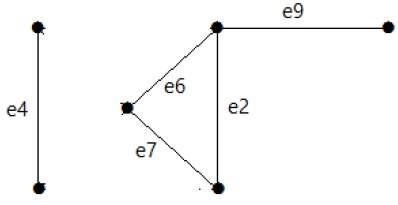
同样,还有其他割集可以断开图 −
E3 = {e9} – 图的最小割集。
E4 = {e3, e4, e5}
边连通性
假设"G"为连通图。移除使"G"断开的最小边数称为 G 的边连通性。
符号 − λ(G)
换句话说,G 的最小割集中的边数称为 G 的边连通性。
如果"G"有割边,则 λ(G) 为 1。(G 的边连通性。)
示例
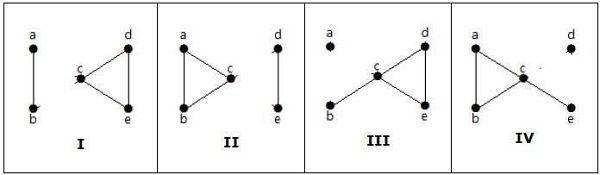
查看下图。通过移除两个最小边,连通图变为断开的。因此,其边连通性 (λ(G)) 为 2。
以下是通过移除两个边 − 来断开图的四种方法
顶点连通性
让"G"成为一个连通图。移除使"G"断开连接或将"G"简化为平凡图的最小顶点数称为其顶点连通性。
符号 − K(G)
示例
在上图中,删除顶点"e"和"i"会使图断开连接。
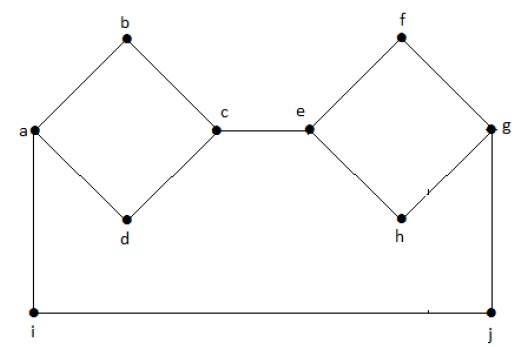
如果 G 有一个割顶点,则 K(G) = 1。
符号 − 对于任何连通图 G,
K(G) ≤ λ(G) ≤ δ(G)
顶点连通性 (K(G))、边连通性 (λ(G))、G 的最小度数 (δ(G))。
示例
计算以下图 − 的 λ(G) 和 K(G)
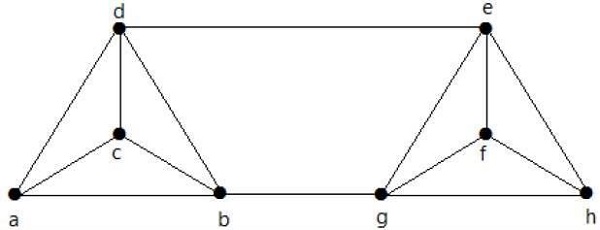
解决方案
从图中,
δ(G) = 3
K(G) ≤ λ(G) ≤ δ(G) = 3 (1)
K(G) ≥ 2 (2)
删除边 {d, e} 和 {b, h},我们可以断开 G。
因此,
λ(G) = 2
2 ≤ λ(G) ≤ δ(G) = 2 (3)
从 (2) 和 (3) 可知,顶点连通性 K(G) = 2


