微波工程 - H 平面三通
H 平面三通结是通过将简单波导连接到已经具有两个端口的矩形波导而形成的。矩形波导的臂形成两个端口,称为共线端口,即端口 1 和端口 2,而新的端口 3 称为侧臂或H 臂。此 H 平面三通也称为分流三通。
由于侧臂的轴与磁场平行,因此此结称为 H 平面三通结。这也称为电流结,因为磁场将其自身分成臂。下图可了解 H 平面 T 型接头的横截面细节。
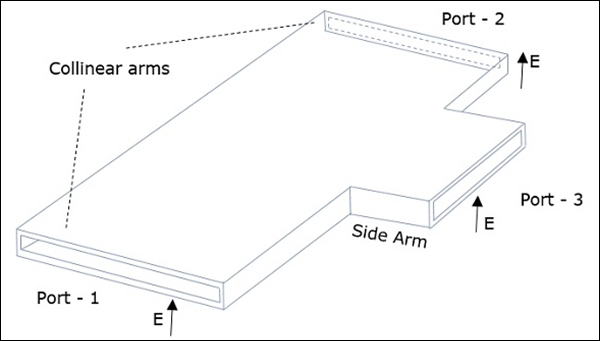
下图显示了侧臂与双向波导的连接,以形成串行端口。
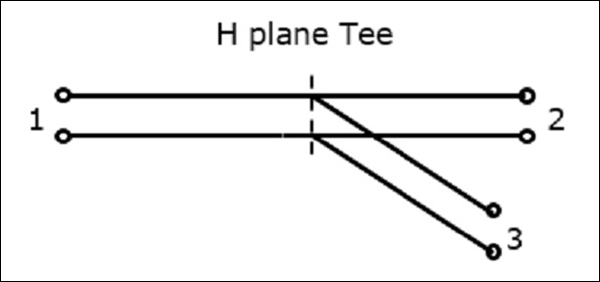
H 平面 T 型接头的属性
H 平面 T 型接头的属性可通过其 $\left [ S ight ]_{3 imes 3}$ 矩阵定义。
它是一个 3×3 矩阵,因为有 3 个可能的输入和 3 个可能的输出。
$[S] = \begin{bmatrix} S_{11}& S_{12}& S_{13}\ S_{21}& S_{22}& S_{23}\ S_{31}& S_{32}& S_{33} \end{bmatrix}$ ........ 公式 1
由于结面在平面上对称,因此散射系数 $S_{13}$ 和 $S_{23}$ 相等。
根据对称性质,
$S_{ij} = S_{ji}$
$S_{12} = S_{21} \: \: S_{23} = S_{32} = S_{13} \: \: S_{13} = S_{31}$
端口完全匹配
$S_{33} = 0$
现在,$[S]$矩阵可以写成,
$[S] = \begin{bmatrix} S_{11}& S_{12}& S_{13}\ S_{12}& S_{22}& S_{13}\ S_{13}& S_{13}& 0 \end{bmatrix}$ ........ 公式 2
我们可以说有四个未知数,考虑到对称性。
从幺正性
$$[S][S]\ast = [I]$$
$$\begin{bmatrix} S_{11}& S_{12}& S_{13}\ S_{12}& S_{22}& S_{13}\ S_{13}& S_{13}& 0 \end{bmatrix} \: \begin{bmatrix} S_{11}^{*}& S_{12}^{*}& S_{13}^{*}\ S_{12}^{*}& S_{22}^{*}& S_{13}^{*}\ S_{13}^{*}& S_{13}^{*}& 0 \end{bmatrix} = \begin{bmatrix} 1& 0& 0\ 0& 1& 0\ 0& 0& 1 \end{bmatrix}$$
相乘可得,
(注意 R 为行,C 为列)
$R_1C_1 : S_{11}S_{11}^{*} + S_{12}S_{12}^{*} + S_{13}S_{13}^{*} = 1$
$\left | S_{11} ight |^2 + \left | S_{12} ight |^2 + \left | S_{13} ight |^2 = 1$ ........ 等式 3
$R_2C_2 : \left | S_{12} ight |^2 + \left | S_{22} ight |^2 + \left | S_{13} ight |^2 = 1$ ......... 公式 4
$R_3C_3 :\left | S_{13} ight |^2 + \left | S_{13} ight |^2 = 1$ ......... 公式 5
$R_3C_1 : S_{13}S_{11}^{*} - S_{13}S_{12}^{*} = 0$ ......... 公式 6
$2\left | S_{13} ight |^2 = 1 \quad 或 \quad S_{13} = \frac{1}{\sqrt{2}}$ ......... 公式 7
$\left | S_{11} ight |^2 = \left | S_{22} ight |^2$
$S_{11} = S_{22}$ ......... 公式 8
从公式 6 可知,$S_{13}\left ( S_{11}^{*} + S_{12}^{*} ight ) = 0$
因为, $S_{13} eq 0,S_{11}^{*} + S_{12}^{*} = 0,\: 或 \: S_{11}^{*} = -S_{12}^{*}$
或者 $S_{11} = -S_{12} \:\: 或 \:\: S_{12} = -S_{11}$......... 等式 9
在等式 3 中使用这些,
由于, $S_{13} eq 0,S_{11}^{*} + S_{12}^{*} = 0,\: 或 \: S_{11}^{*} = -S_{12}^{*}$
$\left | S_{11} ight |^2 + \left | S_{11} ight |^2 + \frac{1}{2} = 1 \quad 或 \quad 2\left | S_{11} ight |^2 = \frac{1}{2} \quad 或 \quad S_{11} = \frac{1}{2}$..... 公式 10
根据公式 8 和 9,
$S_{12} = -\frac{1}{2}$......... 公式 11
$S_{22} = \frac{1}{2}$......... 公式 12
用 $S_{13}$、$S_{11}$ 代替, $S_{12}$ 和 $S_{22}$ 来自方程 7 和方程 2 中的 10、11 和 12,
我们得到,
$$\left [ S ight ] = \begin{bmatrix} \frac{1}{2}& -\frac{1}{2}& \frac{1}{\sqrt{2}}\ -\frac{1}{2}& \frac{1}{2}& \frac{1}{\sqrt{2}}\ \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}& 0 \end{bmatrix}$$
我们知道 $[b]$ = $[s] [a]$
$$\begin{bmatrix}b_1 \ b_2 \ b_3 \end{bmatrix} = \begin{bmatrix} \frac{1}{2}& -\frac{1}{2}& \frac{1}{\sqrt{2}}\ -\frac{1}{2}& \frac{1}{2}& \frac{1}{\sqrt{2}}\ \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}& 0 \end{bmatrix} \begin{bmatrix} a_1\ a_2\ a_3 \end{bmatrix}$$
这是 H-Plane Tee 的散射矩阵,它解释了其散射特性。


