PyTorch - 线性回归

在本章中，我们将重点介绍使用 TensorFlow 实现线性回归的基本示例。 逻辑回归或线性回归是一种用于对有序离散类别进行分类的监督机器学习方法。 本章的目标是建立一个模型，用户可以通过该模型预测预测变量与一个或多个自变量之间的关系。

这两个变量之间的关系被认为是线性的，即如果 y 是因变量，x 被认为是自变量，那么两个变量的线性回归关系将类似于下面提到的方程 −

Y = Ax+b

接下来，我们将设计一个线性回归算法，它使我们能够理解下面给出的两个重要概念 −

• 成本函数
• 梯度下降算法

下面提到线性回归的示意图

解释结果

$$Y=ax+b$$

• The value of a is the slope.

• The value of b is the y − intercept.

• r is the correlation coefficient.

• r² is the correlation coefficient.

下面提到线性回归方程的图形视图 −

以下步骤用于使用 PyTorch 实现线性回归 −

步骤 1

使用以下代码在 PyTorch 中导入必要的包以创建线性回归 −

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
import seaborn as sns
import pandas as pd
%matplotlib inline

sns.set_style(style = 'whitegrid')
plt.rcParams["patch.force_edgecolor"] = True

步骤 2

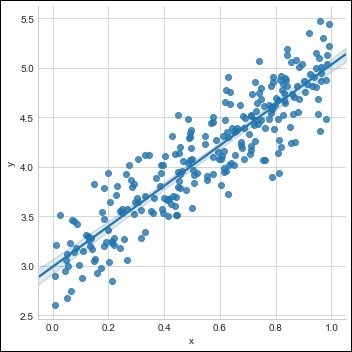
使用可用数据集创建单个训练集，如下所示 −

m = 2 # slope
c = 3 # interceptm = 2 # slope
c = 3 # intercept
x = np.random.rand(256)

noise = np.random.randn(256) / 4

y = x * m + c + noise

df = pd.DataFrame()
df['x'] = x
df['y'] = y

sns.lmplot(x ='x', y ='y', data = df)

步骤 3

使用 PyTorch 库实现线性回归，如下所述 −

import torch
import torch.nn as nn
from torch.autograd import Variable
x_train = x.reshape(-1, 1).astype('float32')
y_train = y.reshape(-1, 1).astype('float32')

class LinearRegressionModel(nn.Module):
   def __init__(self, input_dim, output_dim):
      super(LinearRegressionModel, self).__init__()
      self.linear = nn.Linear(input_dim, output_dim)

   def forward(self, x):
      out = self.linear(x)
      return out
input_dim = x_train.shape[1]
output_dim = y_train.shape[1]
input_dim, output_dim(1, 1)
model = LinearRegressionModel(input_dim, output_dim)
criterion = nn.MSELoss()
[w, b] = model.parameters()

def get_param_values():
   return w.data[0][0], b.data[0]

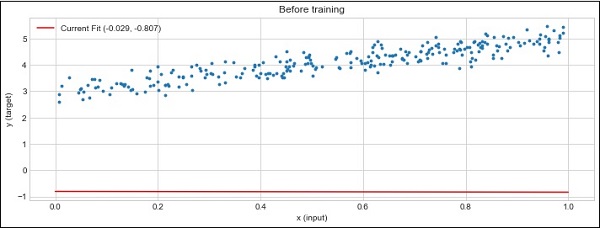
def plot_current_fit(title = ""):
plt.figure(figsize = (12,4))
plt.title(title)
plt.scatter(x, y, s = 8)
w1 = w.data[0][0]
b1 = b.data[0]
x1 = np.array([0., 1.])
y1 = x1 * w1 + b1
plt.plot(x1, y1, 'r', label = 'Current Fit ({:.3f}, {:.3f})'.format(w1, b1))
plt.xlabel('x (input)')
plt.ylabel('y (target)')
plt.legend()
plt.show()
plot_current_fit('Before training')

生成的图如下 −