控制系统 - 波特图
波特图或波特图由两个图组成 −
- 幅度图
- 相位图
在这两个图中,x 轴代表角频率(对数刻度)。而 yaxis 表示幅度图中开环传递函数的幅度(线性标度),以及相位图中开环传递函数的相位角(线性标度)。
以 dB 为单位的开环传递函数的幅度为 -
$$M=20\:\log|G(j\omega)H(j\omega)|$$
以度为单位的开环传递函数的相位角为 -
$$\phi=\angle G(j\omega)H(j\omega)$$
注意 − 对数的底数为 10。
Bode 图基础
下表显示了开环传递函数中存在的项的斜率、幅度和相位角值。绘制 Bode 图时,此数据很有用。
| 术语类型 | G(jω)H(jω) | 斜率(dB/dec) | 幅度 (dB) | 相位角(度) |
|---|---|---|---|---|
常数 |
$K$ |
$0$ |
$20 \log K$ |
$0$ |
原点处的零 |
$j\omega$ |
$20$ |
$20 \log \omega$ |
$90$ |
原点处的'n' 个零 |
$(j\omega)^n$ |
$20\: n$ |
$20\: n \log \omega$ |
$90\: n$ |
极点位于原点 |
$\frac{1}{j\omega}$ |
$-20$ |
$-20 \log \omega$ |
$-90 \: 或 \: 270$ |
'n' 个极点位于原点 |
$\frac{1}{(j\omega)^n}$ |
$-20\: n$ |
$-20 \: n \log \omega$ |
$-90 \: n \: 或 \: 270 \: n$ |
简单零 |
$1+j\omega r$ |
$20$ |
$0\: for\: \omega < \frac{1}{r}$ $20\: \log \omega r\: 对应于 \: \omega > \frac{1}{r}$ |
$0 \: 对应于 \: \omega < \frac{1}{r}$ $90 \: 对应于 \: \omega > \frac{1}{r}$ |
简单极点 |
$\frac{1}{1+j\omega r}$ |
$-20$ |
$0\: 对于\: \omega < \frac{1}{r}$ $-20\: \log \omega r\: 对于\: \omega > \frac{1}{r}$ |
$0 \: 对于 \: \omega < \frac{1}{r}$ 对于\: \omega > \frac{1}{r}$,$-90\: 或 \: 270 \: |
二阶导数项 |
$\omega_n^2\left ( 1-\frac{\omega^2}{\omega_n^2}+\frac{2j\delta\omega}{\omega_n} ight )$ |
$40$ |
$40\:\log\:\omega_n\: 表示 \:\omega < \omega_n$ $20\:\log\:(2\delta\omega_n^2)\: 表示 \:\omega=\omega_n$ $40 \:\log \:\omega\:表示 \:\omega > \omega_n$ |
$0 \: 表示 \:\omega < \omega_n$ $90 \: 表示 \:\omega = \omega_n$ $180 \: 表示 \:\omega > \omega_n$ |
二阶积分项 |
$\frac{1}{\omega_n^2\left ( 1-\frac{\omega^2}{\omega_n^2}+\frac{2j\delta\omega}{\omega_n} ight )}$ |
$-40$ |
$-40\: \log\: \omega_n\: for \: \omega < \omega_n$ $-20\: \log\:(2\delta\omega_n^2)\: 对于 \: \omega=\omega_n$ $-40 \: \log \: \omega\:对于 \:\omega > \omega_n$ |
$-0 \: 对于 \: \omega < \omega_n$ $-90 \: 对于 \: \omega = \omega_n$ $-180 \: 对于 \: \omega > \omega_n$ |
考虑开环传递函数 $G(s)H(s) = K$。
幅度 $M = 20\: \log K$ dB
相位角 $\phi = 0$ 度
如果 $K = 1$,则幅度为 0 dB。
如果 $K > 1$,则幅度为正。
如果 $K < 1$,则幅度将为负值。
下图显示了相应的 Bode 图。


幅度图是一条水平线,与频率无关。当 K 值为 1 时,0 dB 线本身就是幅度图。对于 K 的正值,水平线将向 0 dB 线上方移动 $20 \:\log K$ dB。对于 K 的负值,水平线将向 0 dB 线下方移动 $20\:\log K$ dB。零度线本身是所有 K 正值的相位图。
考虑开环传递函数 $G(s)H(s) = s$。
幅度 $M = 20 \log \omega$ dB
相位角 $\phi = 90^0$
在 $\omega = 0.1$ rad/sec 时,幅度为 -20 dB。
在 $\omega = 1$ rad/sec 时,幅度为 0 dB。
在 $\omega = 10$ rad/sec 时,幅度为 20 dB。
下图显示了相应的 Bode 图。
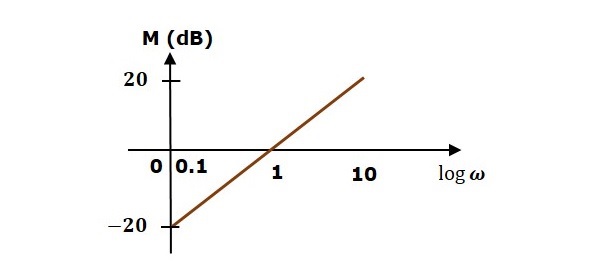

幅度图是一条线,斜率为 20 dB/dec。该线从 $\omega = 0.1$ rad/sec 开始,幅度为 -20 dB,并继续以相同的斜率延伸。它在 $\omega = 1$ rad/sec 处与 0 dB 线相交。在这种情况下,相位图为 900 线。
考虑开环传递函数 $G(s)H(s) = 1 + s au$。
幅度 $M = 20\: log \sqrt{1 + \omega^2 au^2}$ dB
相位角 $\phi = an^{-1}\omega au$ 度
对于 $ω < \frac{1}{ au}$ ,幅度为 0 dB,相位角为 0 度。
对于 $\omega > \frac{1}{ au}$ ,幅度为 $20\: \log \omega au$ dB,相位角为 900。
下图显示了相应的 Bode 图。


幅度图的幅度为 0 dB,最高为 $\omega=\frac{1}{ au}$ rad/sec。从 $\omega = \frac{1}{ au}$ rad/sec 开始,其斜率为 20 dB/dec。在这种情况下,相位图的相位角为 0 度,最高可达 $\omega = \frac{1}{ au}$ rad/sec,从这里开始,相位角为 900。此波特图称为渐近波特图。
由于幅度和相位图用直线表示,因此精确波特图类似于渐近波特图。唯一的区别是精确波特图将具有简单的曲线而不是直线。
同样,您可以为表中给出的开环传递函数的其他项绘制波特图。


