如何使用 Python – Matplotlib 计算和绘制函数的导数?
函数的导数是微积分中使用的关键概念之一。它是衡量函数在改变输出时变化程度的指标。
而 Matplotlib 是 Python 的绘图库,由于它没有提供直接的方法来计算函数的导数,因此您需要使用 NumPy,它也是 Python 库之一,您可以使用它来计算函数的导数,并使用 Matplotlib 来可视化结果。
在本文中,我们将使用 NumPy 库计算函数的导数,并在 Python 中借助 Matplotlib 对其进行可视化。
什么是函数的导数?
导数是函数相对于其输入的变化率。它给出函数在任意点的切线斜率,也可用于查找最大值、最小值、临界点和拐点。函数 f(x) 的导数定义为 x 的变化趋近于零时差商的极限。解释它的数学表达式如下:
f`(x) = lim (h -> 0) [(f(x + h) – f(x)) / h]
此处,极限表示函数在 x 处的瞬时变化率。
Python 中的 Matplotlib 是什么?
Matplotlib 是 Python 最流行的可视化库之一。它在科学计算社区中被广泛使用。它支持多种绘图类型并提供许多自定义选项,还与 NumPy 和其他科学计算库集成。
使用 Matplotlib 计算函数导数
由于 Matplotlib 中没有任何直接方法来计算函数的导数,因此我们需要使用公式来计算导数,并使用图形绘制结果。请按照以下步骤进行操作 -
步骤 1- 首先导入所需的模块,即 matplotlib 和 numpy。
import numpy as np import matplotlib.pyplot as plt
步骤 2 - 导入模块后,定义要区分的函数。让我们取 f(x) = x2
Def f(x): return x**2
步骤 2 – 现在,定义绘制函数和导数的 x 值范围。让我们取 [-4, 4] 的范围
x = np.linspace(-4, 4, 1000)
步骤 3 – 然后,使用 numpy 的 gradient() 函数,我们可以计算函数的导数。此函数的工作是计算值数组的数值梯度,这是导数的近似值。
dfdx = np.gradient(f(x), x)
步骤 4 – 为了绘制原始函数及其导数,我们将使用 matplotlib。将创建一个图作为输出。
plt.plot(x, f(x), label = ‘f(x)’) plt.plot(x, dfdx, label = ‘df/dx’) plt.legend() plt.show()
示例
完成所有步骤后,代码和输出将如下所示:
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return x**2
x = np.linspace(-2, 2, 100)
dfdx = np.gradient(f(x), x)
plt.plot(x, f(x), label='f(x)')
plt.plot(x, dfdx, label='df/dx')
plt.legend()
plt.show()
输出
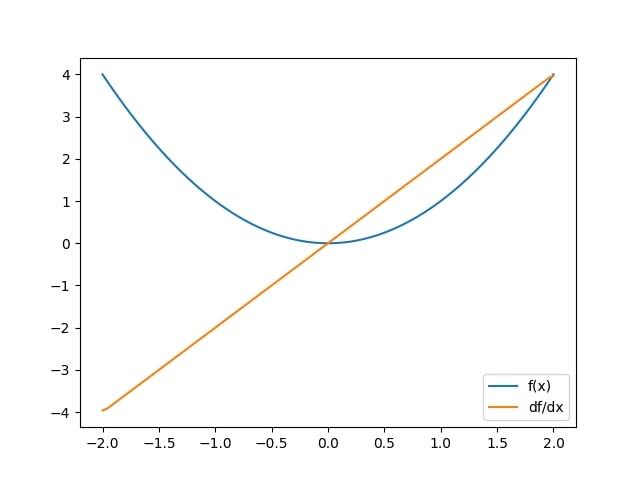
示例
在这里,我们首先将函数定义为 f(x) = sin(x),然后使用 NumPy 的梯度函数计算其导数。然后,我们将尝试使用 Matplotlib 的 plot() 函数绘制原始函数 f(x) 和导数 df/dx。
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return np.sin(x)
x = np.linspace(-np.pi, np.pi, 1000)
dfdx = np.gradient(f(x), x)
fig, ax = plt.subplots()
ax.plot(x, f(x), label='f(x)')
ax.plot(x, dfdx, label="df/dx")
ax.legend()
plt.show()
输出
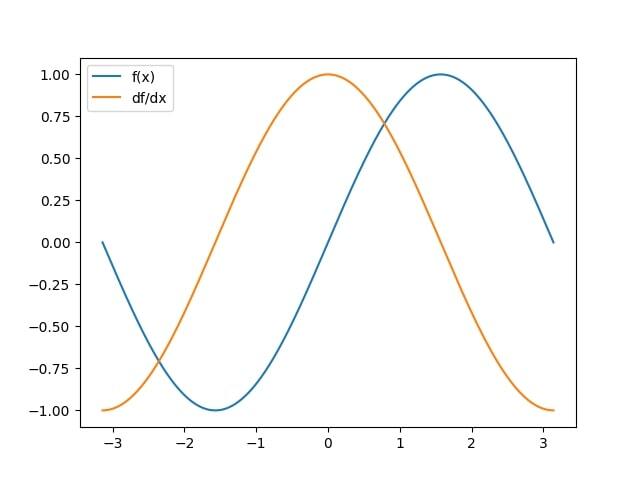
示例
第一步是使用 numpy 幂函数定义我们要微分的函数。然后,为了计算函数在一组点处的导数,我们将使用 gradient() 函数。
此函数的作用是获取一个值数组,然后返回一个具有相同形状的数组,该数组具有给定值的数值导数。
import matplotlib.pyplot as plt
import numpy as np
def f(x):
return np.power(x, 2)
x = np.linspace(0, 4, 100)
y = f(x)
dy = np.gradient(y, x)
plt.plot(x, y, label='f(x)')
plt.plot(x, dy, label="f'(x)")
plt.legend()
plt.show()
输出
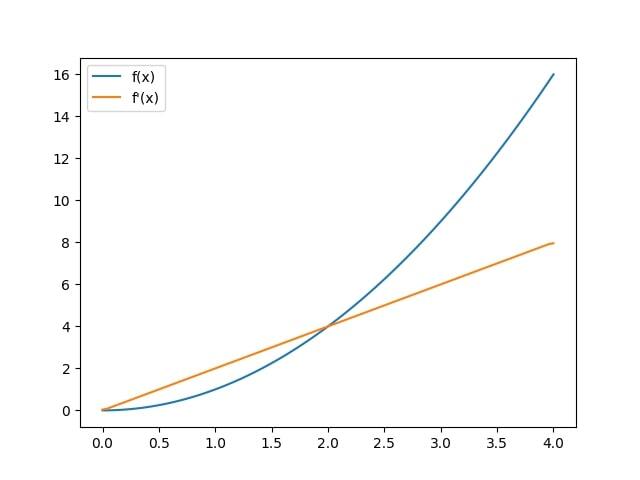
在这里,在每种情况下,我们首先定义了要计算导数的函数。我们使用 numpy 中的 linspace() 函数创建了 x 轴值,并使用它们来计算导数值。最后,我们使用 plot 函数绘制函数及其导数,并使用 legend 函数向图形添加图例。
结论
在本文中,我们使用 python – Matplotlib 计算了函数的导数。我们使用了不同的函数,例如 gradient() 来计算导数,linspace() 用于值的范围,plot() 分别用于绘制函数及其导数。


