OpenCV Python - 傅里叶变换

傅里叶变换，表示能将满足一定条件的某个函数表示成三角函数（正弦和/或余弦函数）或者它们的积分的线性组合。

傅立叶变换用于通过将图像分解为正弦分量和余弦分量，将图像从空间域变换到频域。

在数字图像的情况下，基本灰度图像值通常在 0 到 255 之间。因此，傅里叶变换也需要是离散傅里叶变换 (DFT)。 它用于查找频域。

在数学上，二维图像的傅里叶变换表示如下 −

$$\mathrm{F(k,l)=\displaystyle\sum\limits_{i=0}^{N-1}\: \displaystyle\sum\limits_{j=0}^{N-1} f(i,j)\:e^{-i2\pi (\frac{ki}{N},\frac{lj}{N})}}$$

如果振幅在短时间内变化快，就可以说它是高频信号。 如果变化缓慢，则为低频信号。

在图像的情况下，振幅在边缘点或噪声处变化很大。 所以边缘和噪声是图像中的高频内容。 如果幅度没有太大变化，则为低频分量。

OpenCV 为此提供了函数 cv.dft() 和 cv.idft()。

cv.dft() 执行一维或二维浮点数组的离散傅里叶变换。 相同的命令如下 −

cv.dft(src, dst, flags)

这里，

• src − 可以是实数或复数的输入数组。
• dst − 大小和类型取决于标志的输出数组。
• flags − 转换标志，代表 DftFlags 的组合。

cv.idft() 计算一维或二维数组的逆离散傅里叶变换。 相同的命令如下 −

cv.idft(src, dst, flags)

为了获得离散傅立叶变换，将输入图像转换为 np.float32 数据类型。 获得的变换然后用于将零频率分量移动到频谱的中心，从中计算幅度频谱。

示例

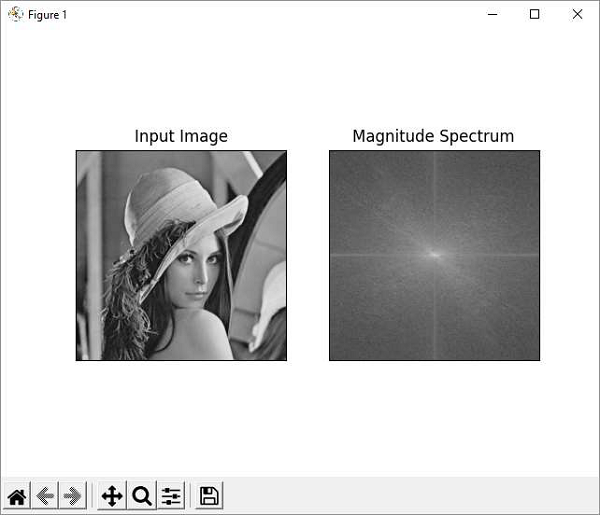
下面给出了使用 Matplotlib 的程序，我们绘制了原始图像和幅度谱 −

import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt
img = cv.imread('lena.jpg',0)
dft = cv.dft(np.float32(img),flags = cv.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)
magnitude_spectrum = 20*np.log(cv.magnitude(dft_shift[:,:,0],dft_shift[:,:,1]))
plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()

输出