数制转换

如您所知，十进制、二进制、八进制和十六进制数制都是位置值数制。要将二进制、八进制和十六进制转换为十进制数，我们只需将每个数字与其位置值的乘积相加即可。在这里，我们将学习这些数制之间的其他转换。

十进制到二进制

通过将数字重复除以 2 并记录余数，可以将十进制数转换为二进制。让我们举个例子来看看这是如何发生的。

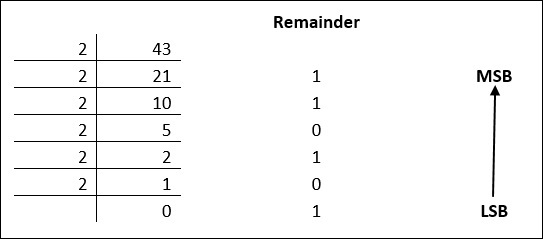
余数要从下往上读才能得到二进制等价数。

43₁₀ = 101011₂

十进制到八进制

通过将数字重复除以 8 并记录余数，可以将十进制数转换为八进制数。让我们举个例子来看看这是如何发生的。

从下到上读取余数，

473₁₀ = 731₈

十进制到十六进制

通过将数字重复除以 16 并记录余数，可以将十进制数转换为八进制。让我们举个例子来看看这是如何发生的。

从下往上读取余数，我们得到，

423₁₀ = 1A7₁₆

二进制转八进制，反之亦然

要将二进制数转换为八进制数，请遵循以下步骤 −

• 从最低有效位开始，将三位分组。

• 如果分组时少了一位或两位，可以在最高有效位后添加 0

• 将每组转换为其等效值八进制数

让我们举一个例子来理解这一点。

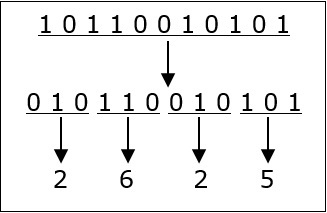
1011001010₁₂ = 2625₈

要将八进制数转换为二进制，每个八进制数字都根据此表转换为其 3 位二进制等价数。

54673₈ = 101100110111011₂

二进制转十六进制

要将二进制数转换为十六进制数，请遵循以下步骤 −

• 从最低有效位开始，将四位分组。

• 如果分组时少了一位或两位，可以在最高有效位后添加 0。

• 将每组转换为其等效的八进制数。

让我们举一个例子来理解这一点。

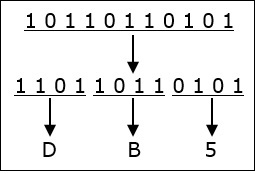
10110110101₂ = DB5₁₆

要将八进制数转换为二进制，每个八进制数字都转换为其 3 位二进制等值数字。