图中的团
最近,基于图的表示法在模拟真实世界数据方面获得了极大的欢迎。团是图论中的一个关键问题,用于解决许多数学问题和创建图。团在计算机科学领域得到了广泛的研究,团问题是评估图中具有一定大小的团是否为 NP 完全的。然而,尽管存在所有复杂性,但仍有几种寻找团的技术进行了研究。
什么是团?
在所有无向图中,G = (N, E),团是"节点的子集",因此所有不同节点对都在附近。指定图的完整子图是无向图中的团。完整子图的所有顶点都与所有其他顶点相连。独立集与补图中的团相反,因为每个团都类似于一个独立集。在考虑所有顶点的情况下找到图的最小团称为团覆盖问题。
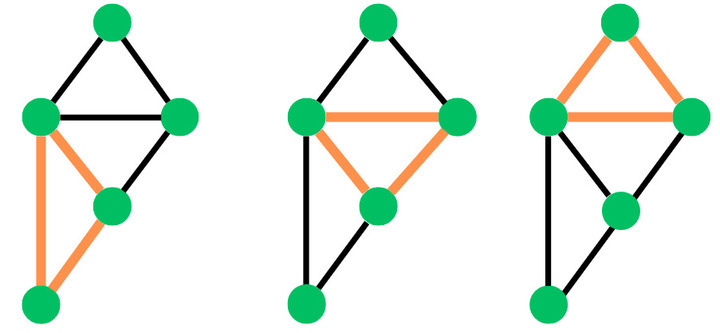
最大团是无法通过添加额外相邻节点进一步扩大的团。
在图中,最大团是指没有团拥有更多顶点的团。此外,图中具有最大团的节点总数称为团数。
因此,最大团被最大程度地团化(但并非总是相反)。
什么是 K 团?
大小为 k 的团称为"k 团"(但是,这个词有时也用于指代距离不超过 k 的最大顶点组)。 0-团表示空集(没有顶点的集合),"1-团"表示节点,2-团表示边,"3-循环"用 3-团表示。
关于团的定理是什么?
根据 Ramsey 定理,任何图或其补图中都存在一个节点数最少为对数的团。
"Turán 定理"限制了密集图的团大小。如果图包含足够的边,则存在巨团。例如,任何具有 m 个节点且边数大于 [m/2][m/2] 的图中都必须存在一个三顶点团。
Moon 和 Moser 确定,在具有 3n 个节点的图中只能存在 3n 个最大团。 Moon-Moser 图满足此限制。
基于团的图分类
各种主要类型的图都可以使用其团来描述或分类 −
图 |
特征 |
|---|---|
"簇图" |
以团为连通分量的图 |
"块图" |
以团为双连通分量的图。 |
"分裂图" |
属于团的每条边至少有一个顶点的图。 |
"无三角形图" |
除了边和顶点之外没有其他团的图 |
"线图" |
图的边可能使用"边不相交团"覆盖,这意味着覆盖中的团中只有两个是每个顶点的成员。 |
团问题
团问题是一项技术任务,您必须在图中定位团。它包括大量基于必须识别团块的位置以及必须获得有关团块的详细信息类型的公式。
识别"最大团块"、定位加权图的"最大权重团块"、识别最大团块以及确定任何图是否包含超过一定大小的团块构成了构建团块问题的核心方法。
解决大多数团块问题都具有挑战性。"Karp 的 21 个 NP 完全"问题之一包括团块选择问题。定位最大团块很复杂,需要设置参数,并且难以量化。此外,由于存在具有大量指数最大团块的图,因此识别每个最大团块可能需要指数时间。
识别单个最大团块
一种简单的贪婪技术可以确定最大的团块。通过迭代图中的所有顶点,从任何团(仅一个节点或可能是整个集合)开始,我们一次一个节点地扩大当前团。对于此迭代检查的每个顶点,如果特定顶点靠近其他每个顶点,则将该顶点添加到团,如果不靠近,则忽略它。该算法在时间上是线性的。由于最大团很容易被发现,并且可能最小化大小,因此人们更加关注发现大团的更困难的计算过程,而不是定位单个最大团的难度。
具有固定大小的团
使用"蛮力"算法,可以确定图中是否包含"k 顶点团",并识别其中包含的每个这样的团。此方法检查每个具有 k 个节点的子图,以检查它是否是团的一部分。在巨大的 O 符号中,它需要 O(nkk2) 时间。这是因为存在"O(nk) 个子图"需要检查,所有这些子图都有"O(k2) 条边"需要验证。因此,当 k 是给定常数时,问题在时间上是多项式的。当 k 没有固定值并且作为问题输入的一部分波动时,时间将呈指数增长。
识别所有最大团
实施"Bron-Kerbosch"方法,以多项式时间识别每个最大团,以及最坏情况下的最佳时间。根据 Moon 和 Moser 的说法,每个 n 顶点网络的最大团伙数不得超过 3n3,而"Bron-Kerbosch"方法(通过关键方法减少每个阶段执行的重复调用次数)的最坏情况执行周期为 O(3n3),符合这一约束。
团伙的应用是什么?
假设一个在线社区,其中图的节点表示人,边表示相互联系。术语"团伙"是指一群彼此熟悉的人。可以使用检测团伙的算法找到这些朋友网络。
Kuhl、Crippen 和 Friesen 在计算化学中使用团伙来表示两个分子结合的点。
为部分陈述的布尔函数创建高效电路。
结论
团伙在图分析中必不可少,经常用于解决数学问题和图形创建。尽管"团伙问题是 NP 完全的",但人们正在研究各种检测团伙的算法。K 团伙是指大小为 k 的团伙,并且存在各种关于团伙的定理。它们在计算机科学、生物信息学和图论中有多种应用。


