中心八边形数
问题陈述包括打印某个正整数 N 的第 N 个中心八边形数,该数由用户提供。
中心八边形数是一种可以用图形模式表示的数字。每个中心八边形数都可以表示为中心的一个点,周围是八边形的连续层。八边形是几何学中的一种多边形,其中有 8 条边。八边形的连续层意味着围绕中心点的第一层将是一个八边形,围绕的第二层将是一个 16 边形,然后是一个 24 边形,依此类推。
因为中心八边形数是一种形象化的数字。让我们借助下图来理解这些数字。

第一个中心八边形数字仅表示为中心的一个点。因此,该数字为 1。
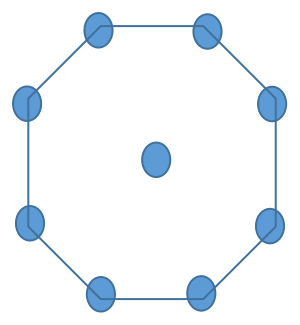
下一个中心八边形数字表示为中心的一个点,周围是一层八边形。因此,数字变为 1+8=9。
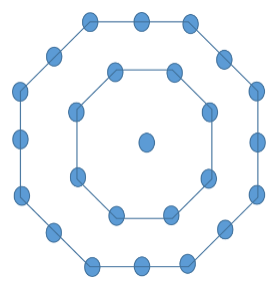
下一个中心八边形数字以图形的形式表示为中心的一个点,周围是 2 个连续的八边形层,即 8 边形和 16 边形。因此,第三个中心八边形数字是 1+8+16=25。
同样,中心八边形数字序列中的下一个数字也以数字表示。按照数字的模式,我们可以计算中心八边形数字序列中的数字。中心八边形数列中的前几个数字是1、9、25、49、81、121、169、225、289……。
在这个问题中,我们将给出任何正整数,即 N。我们的任务是打印中心八边形数相对于 N 的值,即第 N 个中心八边形数。
示例 −
输入:N= 4 输出:49
解释 − 给出的 N 值为 4。相对于 N 的中心八边形数,即第 4 个中心八边形数为 49,可以表示为中心的点被 (N-1) 个连续的八边形层包围。八边形的 3 个连续层分别为 8、16、24。因此,数字为 1+8+16+24=49。
输入:N=7 输出:169
解释 - 与输入值 N 相对应的中心八边形数的值是 169,表示为中心的点,被 (N-1) 个连续的八边形层包围,即 1+8+16+24+32+40+48=169。
让我们了解使用图中遵循的模式计算任何正 N 值的第 N 个中心八边形数的算法。
算法
如果我们观察任何中心八边形数的图形表示所遵循的模式,我们可以得出结论,它是八边形的 (N-1) 个连续层与 1 的总和,其中 N 是第 N 个中心八边形数,1 代表中心的点。
八边形的连续层数为 8、16、24、32、4计算 AP 的 n 项之和,其中首项为 a,公差为 d0……由八边形的连续层形成的序列是一个 AP,其首项为 8(即 a=8),序列中每个项之间的公差也是 8(即 d=8)。
计算 AP 的 n 项之和,其中首项为 a,公差为 d −
$$\mathrm{S_n = \frac{n}{2}(2*a+(n − 1)d)}$$
其中,𝑆𝑛表示 AP 前 n 项之和,a 和 d 分别是 AP 的首项和公差。
我们可以使用此公式计算八边形连续层序列前 (N-1) 项之和,因为它也是计算第 N 个中心八边形数的 AP。
因此,第 N 个中心八边形数可以通过以下公式给出:
$$\mathrm{(Centered \: Octagonal)_N=sum \: of \:(N − 1)successive \: layer \: of \: an \: octagonal +1}$$
通过将值放入上述公式中以计算 AP 的前 n 项之和,可以计算出八边形的 (N-1) 个连续层的总和。
$$\mathrm{(Centered \: Octagonal)_N=\frac {N − 1}{2}(2*a+(N − 2)d)+1}$$
a 即第一项的值是 8,d 即公差也是 8,因为序列是 8、16、24、32……。
$$\mathrm{(Centered \: Octagonal)_N=\frac {(N − 1)}{2}(16+(N − 2)*8)+1}$$
此表达式可以进一步简化为,
$$\mathrm{(centered \: octagonal)_N=\frac {8*(N − 1)}{2}(2+N − 2)+1}$$
$$\mathrm{=4N(N − 1)+1}$$
我们将使用通过中心八边形数的图形表示中遵循的模式得出的表达式来计算我们解决问题的方法中的第 N 个中心八边形数。
方法
在我们的方法中,实现第 N 个中心八边形数公式的步骤如下 -
要计算对于任何输入值 N,创建一个函数,计算第 N 个中心八边形数。
初始化一个名为 ans 的变量,用于存储第 N 个数字的值,该数字将是我们需要的答案。确保变量为 long long 数据类型,以便存储较大 N 值的中心八边形数的值。
使用公式 4𝑁(𝑁 − 1) + 1,我们将计算 N 的中心八边形数并将其存储在 ans 中。
返回变量,即我们需要的输出。
该方法的 C++ 代码 −
示例
//C++ 代码用于打印第 N 个中心八边形数
//对于任何正值的 N
#include <bits/stdc++.h>
using namespace std;
//函数用于计算给定 N 值的第 N 个中心八边形数
long long number(int N){
//long long 数据类型用于存储第 N 个数字的较大值
long long ans; //存储第 N 个中心八边形数
ans = 4*N*(N-1)+1; //使用公式 4N(N-1)+1 计算数字
return ans; //返回存储在 ans 中的值
}
int main(){
int N;
N=14;
//调用函数
cout<<"N="<<N<<" 的中心八边形数为 "<<number(N)<<endl;
N=25;
cout<<"N="<<N<<" 的中心八边形数为 "<<number(N)<<endl;
return 0;
}
输出
N=14 的中心八边形数为 729 N=25 的中心八边形数为 2401
时间复杂度 − O(1) ,因为表达式花费了常数时间来计算第 N 个中心八边形数。
空间复杂度 − O(1) ,因为我们在解决问题时没有使用任何额外空间。
结论
本文讨论了中心八边形数的概念及其图形表示中遵循的模式。我们根据每个中心八边形数的图形模式导出了一个表达式,并在我们的方法中使用这个表达式,以便在 C++ 中在恒定的时间和空间内解决上述问题。
希望您在阅读本文后已经清楚了中心八边形数的所有概念。


