无权图的应用、优点和缺点
图如何工作?
一组相互关联的事物称为图。它们可以表示任何东西,从仅仅基于数学思想到现实生活中的物体、事件和发生。例如,图表示具有家庭关系的个人列表。类似地,大都市网络通过公路连接在一起。
通常,我们将网络元素描述为节点或顶点,而它们之间的链接称为边或弧。
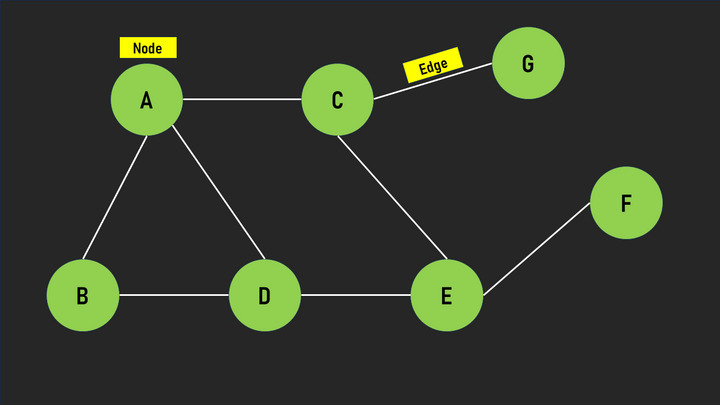
图 1 - 具有节点和边的图形的可视化表示
无加权图:它是什么?
如果任何边都没有附加成本或权重,则称该图为无加权图。它们仅显示两个顶点之间存在关系。
简单来说,当我们关注两个节点是连接还是断开连接时,我们将网络称为无加权网络。我们将节点之间有边的节点称为相邻或相邻。
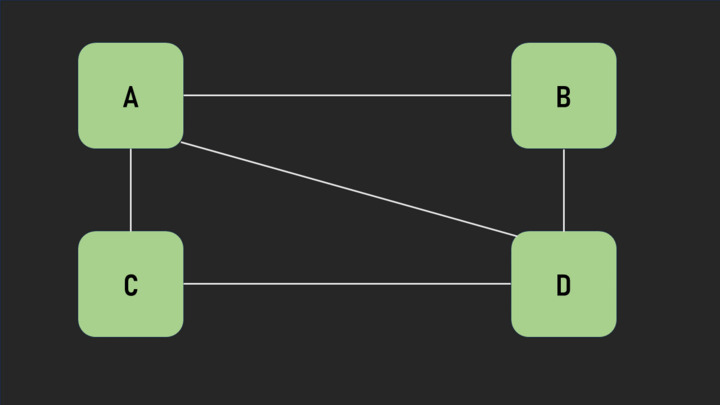
图 2 - 无权图
在本出版物中,我们将研究无权图的简单性,其中顶点的关系显示没有边权重的复杂性。无权图在许多不同领域有广泛的用途,包括网站和社交网络。了解这种形式的图的优点和缺点,以及它在解决问题中的应用。
无权图:优点
由于无权图考虑了任意两个节点之间是否存在连接,因此这些概念很容易阅读和理解。
无权图比加权图占用的存储空间更少,因为它们只需要很少的内存来保存有关边存在的数据。
无权图很容易理解,因为它们描述了连接的存在,不需要分析边权重。
可以使用无权图实现树数据结构。
包括 DFS 和 BFS 在内的几种算法都使用无权图。
有助于实现最佳可视化具有联系但大小不可比的问题。
由于不需要存储或处理边权重,因此非加权图比加权图更容易处理。
非加权图适用于边权重不相关或未知的问题。
当边权重不重要或不清楚时,非加权图是最佳选择。
非加权图比加权图更易于管理,因为它们不需要存储或操作边权重。
非加权图:缺点
非加权图无法描述某些连接,包括图中两个节点之间的成本或分离。
非加权图没有边权重。因此,对于需要了解节点之间的距离或评估最短路径的目的来说,它毫无用处。
鉴于它们无法提供有关节点之间连接的值或强度的详细信息,非加权图可能比加权图更不具洞察力。
无加权图:应用
使用无加权图显示大小上彼此没有关系的统计数据。
无加权图表示计算过程的流程。
图片的分割可以用节点和边来表示,其中节点表示像素,边表示邻接连接。
AI 可以使用状态空间表示来解决问题和做出选择。
工作场所中的数据网络表示,例如万维网。
实时使用无加权图
可以使用无加权图解决难题。
此功能可用于确定社交网络平台上的两个不同的人是否相互关联。
它用于汉密尔顿图中,具有多种现实世界用途,包括基因组映射,以结合几小段遗传信息。
电路的示意图可以用以下表示这个。
无权图用于描述游戏场景中的每个潜在动作。
由于它以无权图的形式表示社交网络中人与人之间的联系,因此它被用于社交媒体平台。
邻接矩阵
邻接矩阵是说明无权图的有效方法。矩阵是一个由 1 和 0 组成的 'n' x 'n' 数组,其中 'n' 是节点总数。如果与元素 $\mathrm{a_{ij}}$ 关联的值为 1,则存在连接第 i 个和第 j 个节点的边。事实上,如果 $\mathrm{a_{ij} \: = \: 0}$,则没有边连接两个节点。
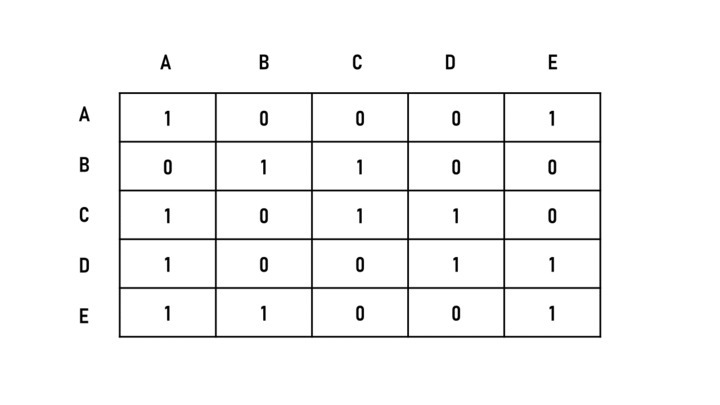
图 3 - 示例邻接矩阵
两个基本假设决定了矩阵表示
通过将节点映射到整数,可以为每个节点赋予不同的整数。在上述情况下,映射为 A 到 1、B 到 2、C 到 3、D 到 4 和 E 到 5。
考虑到可用内存有足够的空间容纳它,可以使用总节点数为 n×n 矩阵分配连续内存。
注意 - 如果这些假设不准确或图形看起来很稀疏,则使用邻接表。
邻接列表
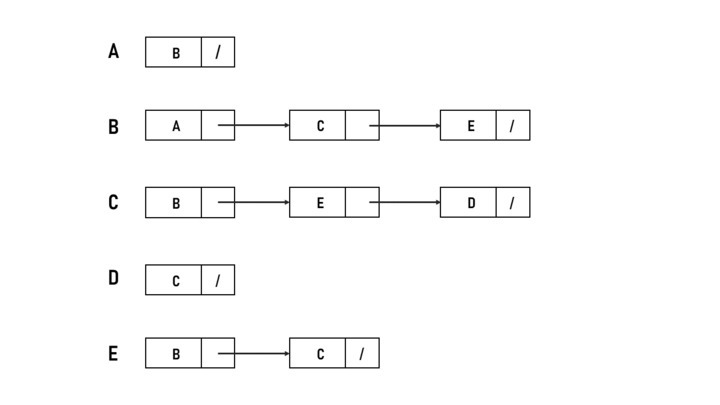
图片 4 - 示例邻接列表
您可以在链接列表中跟踪每个节点的邻居。这种方法的主要优点是用于存储图形数据的内存量不需要是连续的。但是,我们确实失去了矩阵表示的"O(1)"访问复杂性,这是一个宝贵的特性。
无论 i 和 j 的实际值如何,我们都可以在一致的时间内查询"aij"并获取有关第 i 个和第 j 个节点的邻接关系的数据。我们可以使用链接列表浏览整个列表。在最不希望的情况下,搜索查询中的第 j 个顶点以外的所有顶点都是第 i 个节点的邻居。因此,要确定这两个节点是否没有连接,我们将检查链接列表中找到的 [ n - 2 ∈ O(n)] 项。
结论
本文已解决未加权图形表示问题。当我们只需要了解两个事物是否通过边直接连接时,这种图表非常有效。


