XGBoost - 分位数回归

XGBoost 用于一次预测一个主要值，例如所有可能结果的平均值。有时，我们会尝试了解每一种可能性，包括最坏情况和最佳情况。这就是分位数回归的用途。

这就是分位数损失函数用于训练独立 XGBoost 模型的方式。例如，您可以训练 0.05、0.5 和 0.95 分位数的模型，以获得预测区间的下限和上限。

由于分位数回归，除了平均值之外，我们还可以预测数据中的其他点或"分位数"。例如:第 10 个百分位数(较差的结果)、第 50 个百分位数(平均结果)和第 90 个百分位数(可接受的结果)。

XGBoost 中的分位数回归如何工作?

XGBoost 通过将其预测集中在平均值上来定期减少错误。当我们将 XGBoost 与分位数回归结合使用时，我们会调整错误测量。我们不会关注总误差，而是强调特定分位数与预测之间的差距。

简而言之，使用 XGBoost 的分位数回归 −

• 它会预测给定百分位数的值。

• 对于许多情况，我们可以计算可能的结果(坏、平均和好)。

例如，当涉及财务估算时，这在为最佳和最坏情况制定策略时非常有用。

使用 XGBoost 的分位数回归

我们将导入所需的库，在 XGBoost 的帮助下构建分位数回归以生成预测区间。

import xgboost as xgb
import numpy as np
import matplotlib.pyplot as plt

对于训练和测试，在合成数据的帮助下，从随机分布生成目标和特征。

# 生成合成数据
np.random.seed(42)
X_train = np.random.rand(100, 10)
y_train = np.random.rand(100)
X_test = np.random.rand(20, 10)

为了计算满足 XGBoost 回归器目标所需的梯度和 Hessian，创建了一个自定义的分位数损失函数。使用三个不同的分位数来训练模型 - 0.05、0.5(中位数)和 0.95。这些分位数分别与预测区间的下限、中位数和上限相关。训练后，每个分位数都会对测试集做出预测。

def quantile_loss(quantile_value):
   def loss(true_values, predicted_values):
      error = true_values - predicted_values
      gradient = np.where(error > 0, quantile_value, quantile_value - 1)
      # Hessian 是常数
      hessian = np.ones_like(error)  
      return gradient, hessian
   return loss

quantile_levels = [0.05, 0.5, 0.95]
regression_models = {}

for quantile in quantile_levels:
   regressor = xgb.XGBRegressor(objective=quantile_loss(quantile))
   regressor.fit(X_train, y_train)
   regression_models[quantile] = regressor

# 预测分位数
predictions_05 = predictions_models[0.05].predict(X_test)
predictions_50 = predictions_models[0.5].predict(X_test)
predictions_95 = predictions_models[0.95].predict(X_test)

# 下限和上限
lower_prediction = predictions_05
upper_prediction = predictions_95
median_prediction = predictions_50

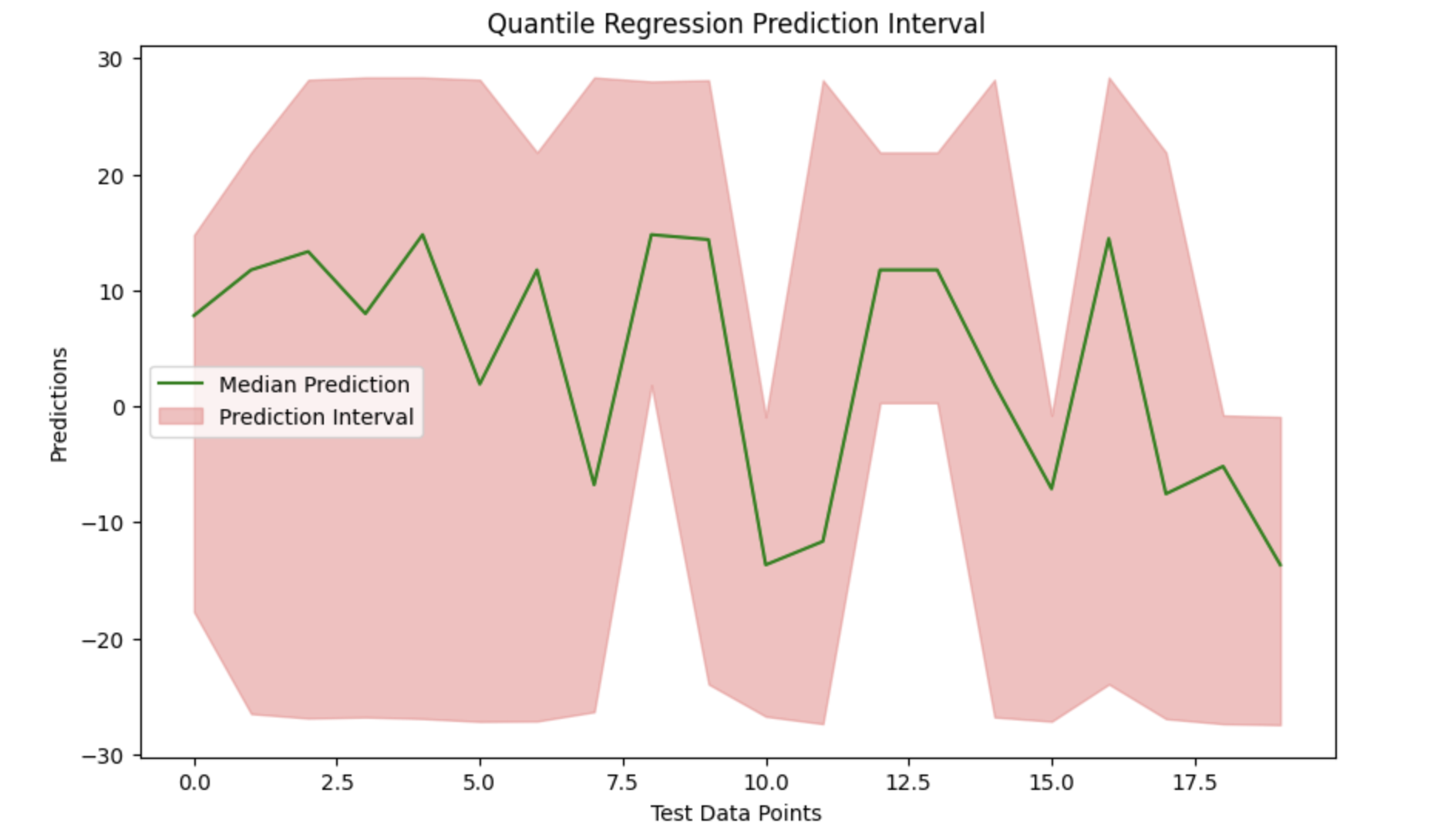
我们可以通过绘制中位数预测并填补上下边界之间的空白来查看数据并有效地显示中位数预测周围的预测区间。

# 可视化
plt.figure(figsize=(10, 6))
plt.plot(median_prediction, label='Median Prediction', color='green')
plt.fill_between(range(len(median_prediction)), lower_prediction, upper_prediction, color='lightcoral', alpha=0.5, label='预测区间')
plt.title('分位数回归预测区间')
plt.xlabel('测试数据点')
plt.ylabel('预测')
plt.legend()
plt.show()

输出

以下是上述模型的结果 −