建模与仿真 - 验证与确认

模拟分析师面临的一个实际问题是验证模型。只有当模型准确表示实际系统时，模拟模型才有效，否则无效。

确认和验证是任何模拟项目中验证模型的两个步骤。

• 验证是比较两个结果的过程。在此过程中，我们需要将概念模型的表示与实际系统进行比较。如果比较结果为真，则有效，否则无效。

• 确认是比较两个或多个结果以确保其准确性的过程。在此过程中，我们必须将模型的实现及其相关数据与开发人员的概念描述和规范进行比较。

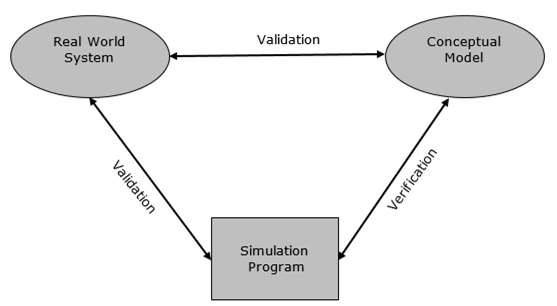
验证和确认技术

有多种技术可用于执行仿真模型的验证和确认。以下是一些常见的技术 −

执行仿真模型验证的技术

以下是执行仿真模型验证的方法 −

• 通过使用编程技能在子程序中编写和调试程序。

• 通过使用"结构化演练"策略，其中不止一个人阅读程序。

• 通过跟踪中间结果并将其与观察到的结果进行比较。

• 通过使用各种输入组合检查仿真模型输出。

• 通过将最终模拟结果与分析结果进行比较。

执行仿真模型验证的技术

步骤 1 − 设计一个具有高有效性的模型。这可以通过以下步骤实现 −

• 在设计时必须与系统专家讨论模型。
• 模型必须在整个过程中与客户互动。
• 输出必须由系统专家监督。

步骤 2 − 在假设数据上测试模型。这可以通过将假设数据应用到模型中并进行定量测试来实现。还可以进行敏感分析，以观察当输入数据发生重大变化时结果变化的影响。

步骤 3 − 确定模拟模型的代表性输出。这可以通过以下步骤实现 −

• 确定模拟输出与实际系统输出的接近程度。

• 可以使用图灵测试进行比较。它以系统格式呈现数据，只有专家才能解释。

• 可以使用统计方法将模型输出与实际系统输出进行比较。

模型数据与实际数据的比较

模型开发后，我们必须将其输出数据与实际系统数据进行比较。以下是执行此比较的两种方法。

验证现有系统

在这种方法中，我们使用模型的实际输入将其输出与实际系统的实际输入进行比较。这个验证过程很简单，但是在执行时可能会出现一些困难，例如如果要将输出与平均长度、等待时间、空闲时间等进行比较，可以使用统计测试和假设检验进行比较。一些统计检验包括卡方检验、Kolmogorov-Smirnov 检验、Cramer-von Mises 检验和矩检验。

验证首次模型

假设我们必须描述一个目前不存在、过去也不存在的提议系统。因此，没有可用的历史数据来比较其性能。因此，我们必须使用基于假设的假设系统。遵循有用的指针将有助于提高其效率。

• 子系统有效性 − 模型本身可能没有任何现有系统可以与之比较，但它可能由已知子系统组成。每个有效性都可以单独测试。

• 内部有效性 −内部方差程度较高的模型将被拒绝，因为高方差的随机系统由于其内部过程会隐藏由于输入变化而导致的输出变化。

• 敏感性分析 − 它提供了系统中需要我们高度关注的敏感参数的信息。

• 表面效度 − 当模型按照相反的逻辑执行时，即使它表现得像真实系统，也应该被拒绝。