Python - 分治法(分而治之)

在分治法(分而治之)中，手头的问题被分成更小的子问题，然后独立解决每个问题。当我们继续将子问题划分为更小的子问题时，我们可能最终会到达无法再划分的阶段。那些"原子"最小的可能子问题（分数）被解决了。最后合并所有子问题的解，以获得原问题的解。

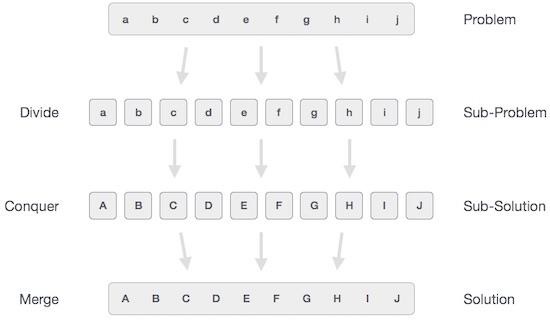
从广义上讲，我们可以通过三步过程来理解分而治之方法。

分割(Divide/Break)

此步骤涉及将问题分解为更小的子问题。子问题应该代表原始问题的一部分。这一步一般采用递归的方式来划分问题，直到没有子问题可以进一步划分。在此阶段，子问题本质上变成了原子问题，但仍代表实际问题的某些部分。

解决(Conquer/Solve)

这一步接收到很多需要解决的小子问题。一般来说，在这个级别，问题被认为是自行"解决"的。

合并(Merge/Combine)

当较小的子问题得到解决时，这个阶段递归地组合它们，直到它们制定出原始问题的解决方案。这种算法方法递归地工作并且解决 &s; 合并步骤非常接近以至于它们看起来像一个。

示例

以下程序是分治法编程方法的示例，其中使用 python 实现了二进制搜索。

二分搜索实现

在二分搜索中，我们采用一个排序的元素列表，并开始在列表的中间寻找一个元素。如果搜索值与列表中的中间值匹配，我们将完成搜索。否则，我们通过根据搜索项的值选择是处理列表的右半部分还是左半部分来删除元素列表的一半。

这是可能的，因为列表是经过排序的，而且它比线性搜索快得多。在这里，我们划分给定的列表并通过选择列表的正确一半来解决。我们重复这种方法，直到我们找到该元素或断定它不在列表中。

示例

def bsearch(list, val):
   list_size = len(list) - 1
   idx0 = 0
   idxn = list_size
# Find the middle most value
   while idx0 <= idxn:
      midval = (idx0 + idxn)// 2
      if list[midval] == val:
         return midval
# Compare the value the middle most value
   if val > list[midval]:
      idx0 = midval + 1
   else:
      idxn = midval - 1
   if idx0 > idxn:
      return None
# Initialize the sorted list
list = [2,7,19,34,53,72]

# Print the search result
print(bsearch(list,72))
print(bsearch(list,11))