神经形态计算 - 架构

神经形态计算机的架构灵感来自人脑的功能，其中神经元和突触作为一个单元共同存储和处理数据。在本节中，我们将讨论神经形态架构的关键组件、工作原理和示例。

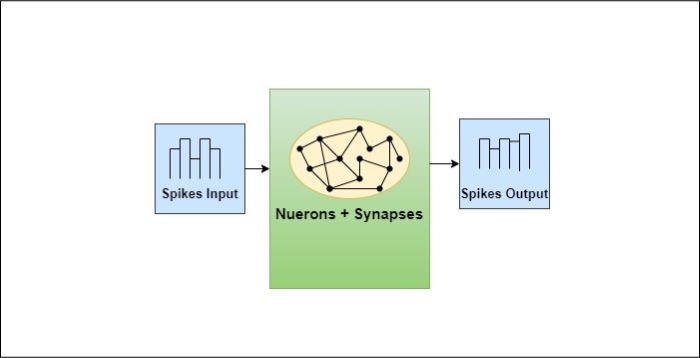
神经形态架构的关键组件

• 神经元:神经形态系统的基本构建块，与生物神经元中的神经元相同。它们通过电脉冲处理信息并进行通信。
• 突触:神经元之间的连接，允许信号传输。神经形态系统利用可变强度的连接来模拟突触可塑性，从而实现学习和记忆形成。
• 神经元层:就像人类大脑被组织成层一样，神经形态架构通常具有多层互连的神经元，允许对信息进行复杂的处理和表示。

神经形态计算机如何工作?

要了解神经形态计算机如何工作，首先需要了解大脑皮层如何运作。大脑皮层是大脑的一部分，人们认为高级认知功能(如感觉知觉、运动命令、空间推理和语言)会发生在这里。

大脑皮层由神经元和突触组成，它们以瞬时速度和令人难以置信的效率从大脑发送和携带信息。神经形态计算机通过使用脉冲神经网络 (SNN) 实现了这种效率。在此处详细了解 SNN。

示例

这是一个基于 Python 的简单代码示例，用于解释神经形态计算背后的概念。此示例将模拟人工神经元如何使用脉冲相互通信，就像神经形态系统中所见的那样。我们将使用脉冲神经网络模型，其中神经元基于阈值发射，突触权重基于简化的学习规则进行调整。

import numpy as np

# 定义参数
NUM_NEURONS = 5 	# 网络中的神经元数量
THRESHOLD = 1.0 	# 神经元的发射阈值
LEARNING_RATE = 0.1 # 突触权重调整速率
TIMESTEPS = 10 		# 模拟步骤数

# 初始化突触权重(神经元之间的连接)
synaptic_weights = np.random.rand(NUM_NEURONS, NUM_NEURONS)

# 初始化神经元状态(0 表示无脉冲，1 表示脉冲)
neuron_states = np.zeros(NUM_NEURONS)

# 简单学习规则:更新突触根据尖峰的权重
def update_weights(pre_neuron, post_neuron):
    if neuron_states[pre_neuron] == 1:  # 前神经元尖峰
        if neuron_states[post_neuron] == 1:  # 后神经元也出现峰值
            # 强化突触(正强化)
            synaptic_weights[pre_neuron, post_neuron] += LEARNING_RATE
        else:
            # 削弱突触(负强化)
            synaptic_weights[pre_neuron, post_neuron] -= LEARNING_RATE
        synaptic_weights[pre_neuron, post_neuron] = np.clip(synaptic_weights[pre_neuron, post_neuron], 0, 1)

# Simulation loop
for t in range(TIMESTEPS):
    print(f"Timestep {t + 1}:")
    
    # 将神经元输入模拟为随机值
    inputs = np.random.rand(NUM_NEURONS)
    
    # 根据输入和突触权重更新神经元状态
    for neuron in range(NUM_NEURONS):
        # 计算从突触到神经元的总输入
        total_input = np.dot(synaptic_weights[:, neuron], neuron_states) + inputs[neuron]
        
        # 确定神经元是否激发(尖峰)
        if total_input > THRESHOLD:
            neuron_states[neuron] = 1  # 神经元激发
        else:
            neuron_states[neuron] = 0  # 神经元不激发
    
    print(f"Neuron states: {neuron_states}")
    print(f"Synaptic weights: 
{synaptic_weights}
")
    
    # 根据脉冲更新突触权重(学习)
    for pre_neuron in range(NUM_NEURONS):
        for post_neuron in range(NUM_NEURONS):
            update_weights(pre_neuron, post_neuron)

解释

这是一个简单的 Python 代码，它实现了赫布学习规则。赫布学习是一种受生物学启发的学习规则，它指出一起激发的神经元会连接在一起。换句话说，如果两个神经元同时活跃，它们之间的连接就会加强。网络由多个通过突触(具有权重)连接的神经元组成，每个神经元都可以根据其接收的总输入"激发"或"激增"。

• 定义参数:最初，我们定义神经网络的所有参数，如神经元数量、阈值和学习率。
• 学习规则:函数 update_weights(pre_neuron, post_neuron):更新两个神经元之间的突触权重。如果前神经元激增，后神经元激增，则权重会增加(正强化)。如果只有前神经元出现脉冲，则权重会降低(负强化)。换句话说，该函数实现了上面提到的"火线连线"函数。
• 模拟循环:在每个时间步骤中，都会为每个神经元生成随机输入值。此输入模拟对神经元的外部刺激。

神经形态芯片示例

• IBM TrueNorth:一种数字神经形态芯片，旨在模拟一百万个神经元和超过 2.56 亿个突触，从而实现复杂的神经网络计算。
• Intel Loihi:一种使用脉冲神经网络模型进行片上学习和实时处理的研究芯片。
• SpiNNaker:一种神经形态计算平台，旨在模拟大规模类脑计算，利用数千个低功耗处理核心。