数字电路 - 逻辑门
数字电子电路以两个逻辑电平的电压运行,即逻辑低和逻辑高。逻辑低对应的电压范围用"0"表示。同样,逻辑高对应的电压范围用"1"表示。
具有一个或多个输入和单个输出的基本数字电子电路称为逻辑门。因此,逻辑门是任何数字系统的基石。我们可以将这些逻辑门分为以下三类。
- 基本门
- 通用门
- 特殊门
现在,让我们逐一讨论每个类别下的逻辑门。
基本门
在前面的章节中,我们了解到布尔函数可以根据需求以乘积之和或乘积之和的形式表示。因此,我们可以通过使用基本门来实现这些布尔函数。基本门是 AND、OR 和 NOT 门。
与门
与门是一种具有两个或更多输入并产生输出的数字电路,该输出是所有这些输入的逻辑 AND。可以选择用符号'.'来表示逻辑与。
下表显示了 2 输入与门的真值表。
| A | B | Y = A.B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
这里 A、B 是输入,Y 是两个输入 AND 门的输出。如果两个输入都是"1",则只有输出 Y 为"1"。对于其余的输入组合,输出 Y 为"0"。
下图显示了 AND 门的符号,它有两个输入 A、B 和一个输出 Y。
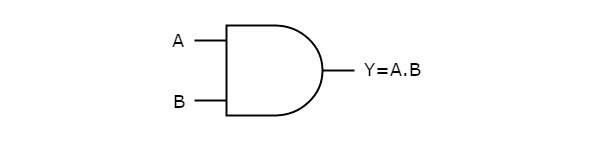
此 AND 门产生一个输出 (Y),它是两个输入 A、B 的逻辑 AND。同样,如果有"n"个输入,则 AND 门产生一个输出,它是所有这些输入的逻辑 AND。这意味着,当所有输入均为"1"时,AND 门的输出将为"1"。
OR 门
OR 门是一种具有两个或多个输入并产生输出的数字电路,该输出是所有这些输入的逻辑或。此逻辑或用符号"+"表示。
下表显示了 2 输入 OR 门的真值表。
| A | B | Y = A + B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
这里 A、B 是输入,Y 是两个输入或门的输出。如果两个输入都是"0",则只有输出 Y 为"0"。对于其余的输入组合,输出 Y 为"1"。
下图显示了或门的符号,它有两个输入 A、B 和一个输出 Y。
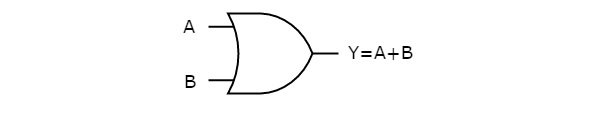
此或门产生一个输出 (Y),它是两个输入 A、B 的逻辑或。类似地,如果有"n"个输入,则或门产生一个输出,它是所有这些输入的逻辑或。这意味着,当这些输入中至少有一个为"1"时,或门的输出将为"1"。
非门
非门是一种具有单个输入和单个输出的数字电路。非门的输出是输入的逻辑反相。因此,非门也称为反相器。
下表显示了非门的真值表。
| A | Y = A’ |
|---|---|
| 0 | 1 |
| 1 | 0 |
这里 A 和 Y 分别是 NOT 门的输入和输出。如果输入 A 为"0",则输出 Y 为"1"。同样,如果输入 A 为"1",则输出 Y 为"0"。
下图显示了 NOT 门的符号,它有一个输入 A 和一个输出 Y。
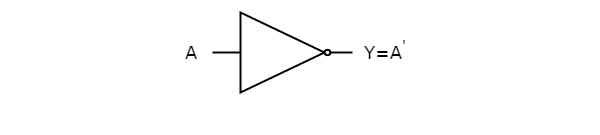
此 NOT 门产生一个输出 (Y),它是输入 A 的补码。
通用门
NAND 和 NOR 门被称为通用门。因为我们可以仅使用 NAND 门来实现任何布尔函数,它是乘积形式的和。类似地,我们可以仅使用 NOR 门来实现任何布尔函数,该函数为和的乘积形式。
NAND 门
NAND 门是一种具有两个或多个输入并产生输出的数字电路,该输出是所有这些输入的逻辑 AND的反转。
下表显示了 2 输入 NAND 门的真值表。
| A | B | Y = (A.B)’ |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
这里 A、B 是输入,Y 是双输入 NAND 门的输出。当两个输入均为"1"时,输出 Y 为"0"。如果至少有一个输入为零,则输出 Y 为"1"。这与双输入 AND 门操作正好相反。
下图显示了 NAND 门的符号,它有两个输入 A、B 和一个输出 Y。
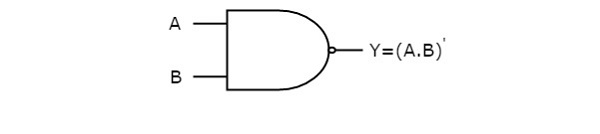
NAND 门操作与 AND 门加上反相器的操作相同。这就是 NAND 门符号如此表示的原因。
NOR 门
NOR 门是一种具有两个或多个输入并产生输出的数字电路,该输出是所有这些输入的逻辑或的反转。
下表显示了 2 输入 NOR 门的真值表
| A | B | Y = (A+B)’ |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
这里 A、B 是输入,Y 是输出。如果两个输入都是"0",则输出 Y 为"1"。如果至少有一个输入为"1",则输出 Y 为"0"。这与两个输入或门操作正好相反。
下图显示了 NOR 门的符号,它有两个输入 A、B 和一个输出 Y。
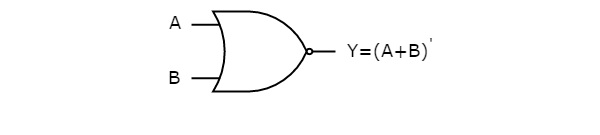
NOR 门操作与后跟反相器的或门相同。这就是 NOR 门符号这样表示的原因。
特殊门
异或门和异或非门被称为特殊门。因为这两个门是或门和异或门的特殊情况。或非门。
异或门
异或门的全称是异或门。除了某些输入有偶数个 1 的情况外,其功能与或门相同。
下表显示了 2 输入异或门的真值表。
| A | B | Y = A⊕B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
这里 A、B 是输入,Y 是两个输入异或门的输出。异或门的真值表前三行与或门的真值表相同。唯一的修改是在第四行。这意味着,当两个输入都是 1 时,输出 (Y) 为零而不是一,因为输入有偶数个 1。
因此,当两个输入中只有一个为"1"时,异或门的输出为"1"。当两个输入相同时,输出为零。
下图显示了异或门的符号,它有两个输入 A、B 和一个输出 Y。
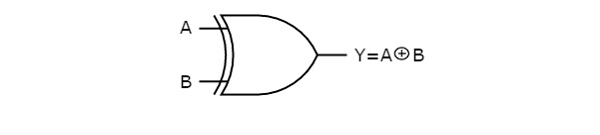
异或门操作与或门类似,只是输入的组合很少。这就是异或门符号如此表示的原因。当输入端有奇数个 1 时,异或门的输出为"1"。因此,异或门的输出也称为奇函数。
异或非门
异或非门的全称是异或非门。除了某些输入端有偶数个 1 的情况外,其功能与或非门相同。
下表显示了 2 输入异或非门的真值表。
| A | B | Y = A⊙B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
这里 A、B 是输入,Y 是输出。前三行 Ex-NOR 门的真值表与 NOR 门的真值表相同。唯一的修改是在第四行。这意味着,当两个输入都是 1 时,输出为 1 而不是 0。
因此,当两个输入相同时,Ex-NOR 门的输出为"1"。当两个输入不同时,输出为 0。
下图显示了 Ex-NOR 门的符号,它有两个输入 A、B 和一个输出 Y。
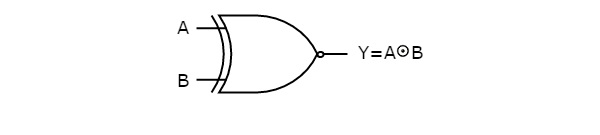
Ex-NOR 门的操作与 NOR 门的操作类似,只是输入的组合很少。这就是 Ex-NOR 门符号这样表示的原因。当输入端有偶数个 1 时,Ex-NOR 门的输出为"1"。因此,Ex-NOR 门的输出也称为偶函数。
从上述 Ex-OR 和 Ex-NOR 逻辑门的真值表中,我们可以很容易地注意到 Ex-NOR 运算只是 Ex-OR 运算的逻辑反转。


