数据科学- 统计方差
方差
方差是另一个数字,表示值的分布程度。
事实上,如果你取方差的平方根,你就会得到标准差。 或者反过来,如果你将标准差乘以它本身,你就会得到方差!
我们将首先使用具有 10 个观测值的数据集来举例说明如何计算方差:
| Duration | Average_Pulse | Max_Pulse | Calorie_Burnage | Hours_Work | Hours_Sleep |
|---|---|---|---|---|---|
| 30 | 80 | 120 | 240 | 10 | 7 |
| 30 | 85 | 120 | 250 | 10 | 7 |
| 45 | 90 | 130 | 260 | 8 | 7 |
| 45 | 95 | 130 | 270 | 8 | 7 |
| 45 | 100 | 140 | 280 | 0 | 7 |
| 60 | 105 | 140 | 290 | 7 | 8 |
| 60 | 110 | 145 | 300 | 7 | 8 |
| 60 | 115 | 145 | 310 | 8 | 8 |
| 75 | 120 | 150 | 320 | 0 | 8 |
| 75 | 125 | 150 | 330 | 8 | 8 |
方差通常由符号 Sigma Square 表示: σ^2
计算方差的第 1 步:求均值
我们要找出 Average_Pulse 的方差。
1.求均值:
(80+85+90+95+100+105+110+115+120+125) / 10 = 102.5
平均值为 102.5
第 2 步:对于每个值 - 求均值的差异
2.找出每个值与平均值的差值:
80 - 102.5 = -22.5
85 - 102.5 = -17.5
90 - 102.5 = -12.5
95 - 102.5 =
-7.5
100 - 102.5 = -2.5
105 - 102.5 = 2.5
110 - 102.5 = 7.5
115 -
102.5 = 12.5
120 - 102.5 = 17.5
125 - 102.5 = 22.5
第 3 步:对于每个差异 - 求平方值
3.求每个差值的平方值:
(-22.5)^2 = 506.25
(-17.5)^2 = 306.25
(-12.5)^2 = 156.25
(-7.5)^2 =
56.25
(-2.5)^2 = 6.25
2.5^2 = 6.25
7.5^2 = 56.25
12.5^2 = 156.25
17.5^2 = 306.25
22.5^2 = 506.25
注意: 我们必须对这些值进行平方才能得到总价差。
第 4 步:方差是这些平方值的平均数
4.对平方值求和并求平均值:
(506.25 + 306.25 + 156.25 + 56.25 + 6.25 + 6.25 + 56.25 + 156.25 + 306.25 +
506.25) / 10 = 206.25
方差为 206.25。
使用 Python 查找 health_data 的方差
我们可以使用 Numpy 的 var() 函数来找到方差(请记住,我们现在使用第一个数据集有 10 个观察值):
实例
import numpy as np
var = np.var(health_data)
print(var)
输出:
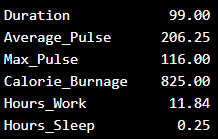
使用 Python 查找完整数据集的方差
这里我们计算整个数据集每一列的方差:
实例
import numpy as np
var_full = np.var(full_health_data)
print(var_full)
输出:


