HTML CSS JAVASCRIPT PYTHON PYTHON2 JAVA C C++ C# SQL Excel Linux AI BOOTSTRAP PHP 教程库 参考手册 技术文章 测验 练习 HOWTO FAQ
❮ 上一节 下一节 ❯

编译器设计 - 语法分析

语法分析或解析是编译器的第二阶段。在本章中，我们将学习解析器构造中使用的基本概念。

我们已经看到，词法分析器可以借助正则表达式和模式规则识别标记。但由于正则表达式的限制，词法分析器无法检查给定句子的语法。正则表达式无法检查平衡标记，例如括号。因此，此阶段使用上下文无关文法 (CFG)，它由下推自动机识别。

另一方面，CFG 是正则文法的超集，如下所示：

CFG 与正则文法的关系

这意味着每个正则文法也是上下文无关的，但存在一些问题，超出了正则文法的范围。 CFG 是描述编程语言语法的有用工具。

上下文无关语法

在本节中，我们将首先了解上下文无关语法的定义，并介绍解析技术中使用的术语。

上下文无关语法有四个组成部分：

  • 一组非终结符 (V)。非终结符是表示字符串集的句法变量。非终结符定义有助于定义语法生成的语言的字符串集。

  • 一组标记，称为终结符 (Σ)。终结符是形成字符串的基本符号。

  • 一组产生式 (P)。语法的产生式指定了终端和非终端组合形成字符串的方式。每个产生式都由一个称为产生式左侧的非终端、一个箭头和一个记号序列和/或非终端（称为产生式的右侧）组成。

  • 其中一个非终端被指定为起始符号 (S)；产生式从这里开始。

字符串是从起始符号派生出来的，方法是用产生式右侧的那个非终端反复替换非终端（最初是起始符号）。

示例

我们以回文语言问题为例，它不能用正则表达式来描述。也就是说，L = { w | w = wR } 不是正则语言。但它可以通过CFG来描述，如下图所示：

G = ( V, Σ, P, S )

其中:

V = { Q, Z, N }
Σ = { 0, 1 }
P = { Q → Z | Q → N | Q → ℇ | Z → 0Q0 | N → 1Q1 }
S = { Q }

此语法描述回文语言，例如：1001、11100111、00100、1010101、11111 等。

语法分析器

语法分析器或解析器以标记流的形式从词法分析器获取输入。解析器根据生成规则分析源代码（标记流）以检测代码中的任何错误。此阶段的输出是解析树。

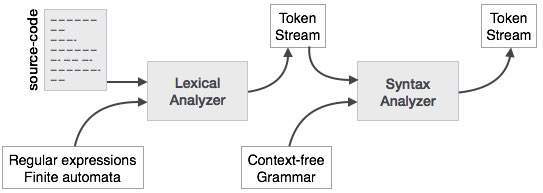
语法分析器

这样，解析器完成两个任务，即解析代码、查找错误并生成解析树作为阶段的输出。

即使程序中存在一些错误，解析器也应该解析整个代码。解析器使用错误恢复策略，我们将在本章后面学习。

派生

派生基本上是一系列产生式规则，目的是获取输入字符串。在解析过程中，我们对输入的某些句子形式做出两个决定：

  • 决定要替换的非终结符。
  • 决定将用哪个生成规则替换非终结符。

要决定用生成规则替换哪个非终结符，我们可以有两个选择。

最左推导

如果从左到右扫描和替换输入的句子形式，则称为最左推导。由最左推导得出的句子形式称为左句子形式。

最右推导

如果我们从右到左扫描并用生成规则替换输入，则称为最右推导。从最右边的推导得到的句子形式称为右句子形式。

示例

产生式规则：

E → E + E
E → E * E
E → id

输入字符串：id + id * id

最左边的推导是：

E → E * E
E → E + E * E
E → id + E * E
E → id + id * E
E → id + id * id

请注意，最左边的非终端总是先处理。

最右边的推导是：

E → E + E
E → E + E * E
E → E + E * id
E → E + id * id
E → id + id * id

解析树

解析树是派生的图形描述。可以方便地看到字符串是如何从起始符号派生出来的。派生的起始符号成为解析树的根。让我们通过上一个主题中的示例来了解这一点。

我们取 a + b * c 的最左派生

最左派生是：

E → E * E
E → E + E * E
E → id + E * E
E → id + id * E
E → id + id * id

步骤 1：

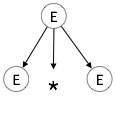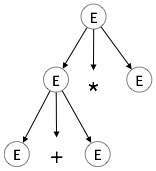E → E * E解析树构造

步骤 2：

E → E + E * E解析树构造

步骤 3：

E → id + E * E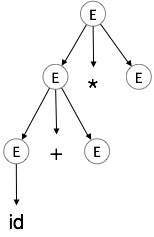解析树构造

步骤 4：

E → id + id * E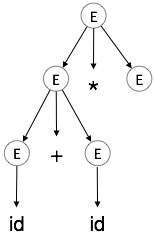解析树构造

步骤 5：

E → id + id * id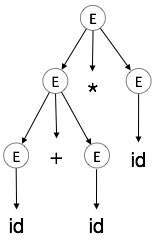解析树构造

在解析树中：

  • 所有叶节点都是终端节点。
  • 所有内部节点都是非终端节点。
  • 按顺序遍历给出原始输入字符串。

解析树描述了运算符的结合性和优先级。首先遍历最深的子树，因此该子树中的运算符优先于父节点中的运算符。

歧义

如果语法 G 对于至少一个字符串有多个解析树（左派生或右派生），则称其为歧义。

示例

E → E + E
E → E – E
E → id

对于字符串 id + id – id，上述语法生成两个解析树：

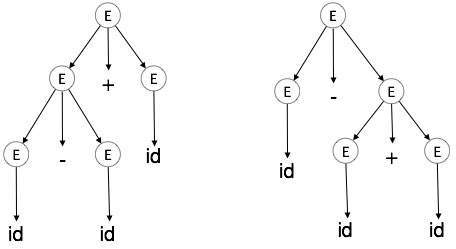
解析树构造

由歧义语法生成的语言被称为固有歧义。语法中的歧义不利于编译器构造。没有方法可以自动检测和消除歧义，但可以通过重写没有歧义的整个语法，或设置并遵循结合性和优先约束来消除歧义。

结合性

如果操作数的两侧都有运算符，则运算符在哪一侧取该操作数由这些运算符的结合性决定。如果运算是左结合的，则操作数将由左运算符获取；如果运算是右结合的，则右运算符将获取操作数。

示例

加法、乘法、减法和除法等运算是左结合的。如果表达式包含：

id op id op id

它将被评估为：

(id op id) op id

例如，(id + id) + id

指数运算等运算是右结合的，即，同一表达式中的评估顺序将是：

id op (id op id)

例如，id ^ (id ^ id)

优先级

如果两个不同的运算符共享一个公共操作数，则运算符的优先级决定哪个将采用该操作数。也就是说，2+3*4 可以有两个不同的解析树，一个对应于 (2+3)*4，另一个对应于 2+(3*4)。通过设置运算符之间的优先级，可以轻松消除此问题。与上例一样，从数学上讲，*（乘法）优先于 +（加法），因此表达式 2+3*4 始终会被解释为：

2 + (3 * 4)

这些方法降低了语言或其语法中出现歧义的可能性。

左递归

如果语法具有任何非终结符"A"，并且其派生包含"A"本身作为最左边的符号，则该语法变为左递归语法。左递归语法被认为是自上而下解析器的问题情况。自上而下的解析器从起始符号开始解析，而起始符号本身是非终结符。所以，当解析器在推导过程中遇到相同的非终结符时，它很难判断何时停止解析左边的非终结符，从而陷入无限循环。

示例：

(1) A => Aα | β

(2) S => Aα | β 
    A => Sd

(1) 是立即左递归的一个例子，其中 A 是任何非终结符，α 表示一串非终结符。

(2) 是间接左递归的一个例子。

左递归

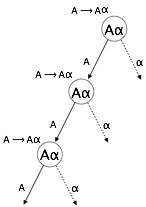
自上而下的解析器将首先解析 A，这反过来会产生一个由 A 本身组成的字符串，解析器可能会永远陷入循环。

删除左递归

删除左递归的一种方法是使用以下技术：

产生式

A => Aα | β

转换为以下产生式

A => βA'
A'=> αA' | ε

这不会影响从语法派生的字符串，但它会删除直接左递归。

第二种方法是使用以下算法，该算法应消除所有直接和间接左递归。

START

Arrange non-terminals in some order like A1, A2, A3,…, An

   for each i from 1 to n
      {
      for each j from 1 to i-1
         {
         replace each production of form Ai ⟹Aj𝜸
         with Ai ⟹ δ1𝜸  | δ2𝜸 | δ3𝜸 |…| 𝜸 
         where Aj ⟹ δ1 | δ2|…| δn  are current Aj productions
         }
      }
   eliminate immediate left-recursion
   
END

示例

生产集

S => Aα | β
A => Sd

应用上述算法后，应变为

S => Aα | β
A => Aαd | βd

然后，使用第一种技术删除直接左递归。

A => βdA'
A' => αdA' | ε

现在，所有产生式都不再具有直接或间接的左递归。

左分解

如果多条语法产生式规则具有共同的前缀字符串，则自上而下的解析器无法选择应采用哪条产生式来解析手头的字符串。

示例

如果自上而下的解析器遇到类似这样的产生式

A ⟹ αβ | α𝜸 | …

然后它无法确定要遵循哪个产生式来解析字符串，因为两个产生式都从同一个终端（或非终端）开始。为了消除这种混淆，我们使用一种称为左分解的技术。

左分解转换语法以使其适用于自上而下的解析器。在这种技术中，我们为每个公共前缀制作一个产生式，其余的派生由新的产生式添加。

示例

上述产生式可以写成

A => αA'
A'=> β | 𝜸 | …

现在解析器每个前缀只有一个产生式，这使得做出决定变得更容易。

第一个和后续集

解析器表构造的一个重要部分是创建第一个和后续集。这些集合可以提供派生中任何终端的实际位置。这样做是为了创建解析表，其中用某些生成规则替换 T[A, t] = α 的决定。

第一组

创建此集合是为了知道非终结符在第一个位置导出哪个终结符。例如，

α → t β

也就是说 α 在第一个位置导出 t（终端）。所以，t ∈ FIRST(α)。

计算第一集的算法

查看 FIRST(α) 集的定义：

  • 如果 α 是终端，则 FIRST(α) = { α }。
  • 如果 α 是非终端且 α → ℇ 是产生式，则 FIRST(α) = { ℇ }。
  • 如果 α 是非终端且 α → 𝜸1 𝜸2 𝜸3 … 𝜸n 且任何 FIRST(𝜸) 包含 t，则 t 在 FIRST(α) 中。

第一集可以看作：

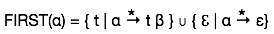
跟随集合

同样，我们计算在产生式规则中哪个终结符号紧跟在非终结符号 α 之后。我们不考虑非终结符可以生成什么，而是看看非终结符生成之后的下一个终结符是什么。

计算跟随集的算法：

  • 如果 α 是起始符号，则 FOLLOW() = $

  • 如果 α 是非终结符并且有生成 α → AB，则 FIRST(B) 属于 FOLLOW(A)，但 ℇ 除外。

  • 如果 α 是非终结符并且有生成 α → AB，其中 B ℇ，则 FOLLOW(A) 属于 FOLLOW(α)。

跟随集可以看作：FOLLOW(α) = { t | S *αt*

语法分析器的局限性

语法分析器以标记的形式从词法分析器接收输入。词法分析器负责语法分析器提供的标记的有效性。语法分析器具有以下缺点 -

  • 它无法确定标记是否有效，
  • 它无法确定标记在使用前是否已声明，
  • 它无法确定标记在使用前是否已初始化，
  • 它无法确定对标记类型执行的操作是否有效。

这些任务由语义分析器完成，我们将在语义分析中研究它。

❮ 上一节 下一节 ❯