编译器设计 - 有限自动机

有限自动机是一种状态机，它将一串符号作为输入，并相应地改变其状态。有限自动机是正则表达式的识别器。当将正则表达式字符串输入到有限自动机中时，它会为每个文字改变其状态。如果输入字符串被成功处理并且自动机达到其最终状态，则该字符串被接受，即刚刚输入的字符串被称为手头语言的有效标记。

有限自动机的数学模型包括：

• 有限状态集 (Q)
• 有限输入符号集 (Σ)
• 一个起始状态 (q0)
• 最终状态集 (qf)
• 转换函数 (δ)

转换函数 (δ) 将有限状态集 (Q) 映射到有限输入符号集 (Σ)，Q × Σ ➔ Q

有限自动机构造

让 L(r) 成为某个有限自动机 (FA) 识别的正则语言。

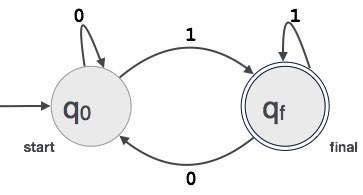
• 状态：FA 的状态用圆圈表示。状态名称写在圆圈内。

• 起始状态：自动机开始的状态称为起始状态。起始状态有一个指向它的箭头。

• 中间状态：所有中间状态至少有两个箭头；一个指向中间状态，另一个从中间状态指向外部。

• 最终状态：如果成功解析输入字符串，则自动机应处于此状态。最终状态用双圆圈表示。它可能有奇数个指向它的箭头和偶数个从中间状态指向外部的箭头。奇数箭头的数量比偶数多一个，即 奇数 = 偶数 + 1。

• 转换：当在输入中找到所需的符号时，就会从一个状态转换到另一个状态。转换后，自动机可以移动到下一个状态或保持在同一状态。从一个状态到另一个状态的移动显示为有向箭头，其中箭头指向目标状态。如果自动机保持在同一状态，则会绘制一个从状态指向自身的箭头。

示例：我们假设 FA 接受以数字 1 结尾的任何三位二进制值。 FA = {Q(q₀, q_f), Σ(0,1), q₀, q_f, δ>