机器学习中带有已解决示例的 K-Medoids 聚类
简介
K-Medoids 是一种使用聚类分区方法的无监督聚类算法。它是 K-Means 聚类算法的改进版本,特别用于处理异常数据。它需要未标记的数据才能使用。
在本文中,让我们通过示例了解 k-Medoids 算法。
K-Medoids 算法
在 K-Medoids 算法中,每个数据点称为中心点。中心点充当聚类中心。中心点是一个点,它与同一聚类中所有其他点的距离总和最小。对于距离,可以使用任何合适的度量,如欧几里得距离或曼哈顿距离。
应用算法后,完整数据被分为 K 个簇。
K-Medoids 有三种类型 - PAM、CLARA 和 CLARANS。 PAM 是最流行的方法。它有一个缺点,就是需要花费大量时间。
K-Medoid 的应用方式是
一个点只能属于一个簇
每个簇至少有一个点
让我们通过一个例子来了解 K-Medoids 的工作过程。
工作
最初,我们将 K 作为簇数,将 D 作为未标记数据。
首先,我们从数据集中选择 K 个点,并将它们分配给 K 个簇。这 K 个点充当初始中心点。每个对象都被放入一个簇中。
接下来,使用欧几里得距离或曼哈顿距离等距离度量来计算初始中心点(点)与其他点(非中心点)之间的距离。等。
非中心点被分配到与中心点距离最小的特定簇中。
现在计算总成本,即簇内其他点到中心点的距离之和。
接下来,选择一个随机的新非中心点对象 s 并将其与初始中心点对象 r 交换,然后重新计算成本。
如果成本 < costr ,则交换变为永久性的。
最后,重复步骤 2 到 6,直到成本不再变化。
示例
让我们考虑以下数据集。我们将取 k=2 和要使用的距离公式
$$\mathrm{D=\mid x_{2}-x_{1}\mid+\mid y_{2}-y_{1}\mid}$$
Sl. no |
x |
y |
|---|---|---|
1 |
9 |
6 |
2 |
10 |
4 |
3 |
4 |
4 |
4 |
5 |
8 |
5 |
3 |
8 |
6 |
2 |
5 |
7 |
8 |
5 |
8 |
4 |
6 |
9 |
8 |
4 |
10 |
9 |
3 |
数据在绘图时看起来与下图类似。
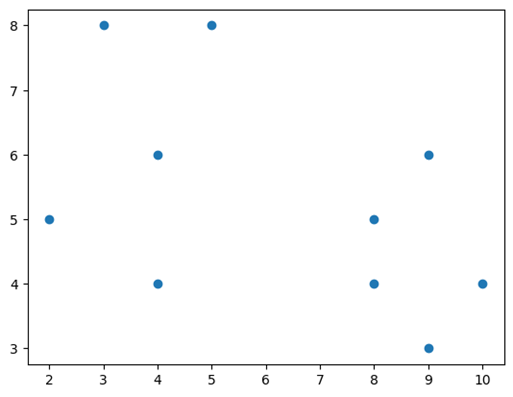
对于 k = 2,我们取两个随机点 P1(8,4) 和 P2(4,6),并计算它们与其他点的距离。
Sl. no |
x |
y |
Dist from P1 (8,4) |
Dist from P2 (4,6) |
|---|---|---|---|---|
1 |
9 |
6 |
3 |
5 |
2 |
10 |
4 |
2 |
8 |
3 |
4 |
4 |
4 |
2 |
4 |
5 |
8 |
7 |
3 |
5 |
3 |
8 |
9 |
3 |
6 |
2 |
5 |
7 |
3 |
7 |
8 |
5 |
1 |
5 |
8 |
4 |
6 |
- |
- |
9 |
8 |
4 |
- |
- |
10 |
9 |
3 |
2 |
8 |
1,2,7,10 - 分配给 P1(8,4)
3,4,5,6 - 分配给 P2(4,6)
总成本 C1 = (3+2+1+2) +(2+3+3+3) = 19
现在让我们随机选择其他两个点作为中心点 P1(8,5) 和 P2(4,6),并计算距离。
Sl. no |
x |
y |
Dist from P1(8,5) |
Dist from P2(4,6) |
|---|---|---|---|---|
1 |
9 |
6 |
2 |
5 |
2 |
10 |
4 |
3 |
8 |
3 |
4 |
4 |
5 |
2 |
4 |
5 |
8 |
6 |
3 |
5 |
3 |
8 |
6 |
3 |
6 |
2 |
5 |
6 |
3 |
7 |
8 |
5 |
- |
- |
8 |
4 |
6 |
- |
- |
9 |
8 |
4 |
1 |
- |
10 |
9 |
3 |
3 |
8 |
$$\mathrm{涉及的新成本\:C_{2}=[2+3+1+3]+[2+3+3+3]=20}$$
$$\mathrm{涉及交换 C 的总成本\:=C_{2}-C_{1}=20-19=1}$$
由于交换 C 的总成本大于 0,我们确实会恢复交换。
点 P1(8,4) 和 P2(4,6) 被视为最终的中心点,仅使用这些点形成 2 个簇。
代码实现
import numpy as np
from sklearn_extra.cluster import KMedoids
data = {'x' : [9,10,4,5,3,2,8,4,8,9],
'y' : [6,4,4,8,8,5,5,6,4,3]}
x = [[i,j] for i,j in zip(data['x'],data['y'])]
data_x = np.asarray(x)
model_km = KMedoids(n_clusters=2)
km = model_km.fit(data_x)
print("标签 :",km.labels_)
print("聚类中心 :",km.cluster_centers_)
输出
标签 : [1 1 0 0 0 0 1 0 1 1] 聚类中心 : [[4. 6.] [8. 4.]]
结论
K-Medoids 是 M-Means 算法的一种改进方法。它是无监督的,需要未标记的数据。K-Mediods 是一种基于距离的方法,它依赖于聚类距离和聚类内距离,其中 medoids 充当聚类中心并作为计算距离的参考点。它非常有用,因为它可以非常有效地处理异常值。


