如何在 Python 中实现梯度下降以找到局部最小值?
梯度下降是机器学习中一种重要的优化方法,用于最小化模型的损失函数。通俗地说,它需要反复更改模型的参数,直到找到最小化损失函数的理想值范围。该方法通过沿着损失函数的负梯度方向(更具体地说,最陡下降路径)进行微小的移动。学习率是一个调节算法在速度和准确性之间权衡的超参数,它会影响步骤的大小。许多机器学习方法,包括线性回归、逻辑回归和神经网络等,都采用梯度下降。它的主要应用是在模型训练中,目标是最小化目标变量的预期值和实际值之间的差异。在这篇文章中,我们将研究如何在 Python 中实现梯度下降以找到局部最小值。
现在是时候在 Python 中实现梯度下降了。以下是有关如何实现它的基本说明 -
首先,我们导入必要的库。
定义函数及其导数。
接下来,我们将应用梯度下降函数。
应用该函数后,我们将设置参数以找到局部最小值,
最后,我们将绘制输出图。
在 Python 中实现梯度下降
导入库
import numpy as np import matplotlib.pyplot as plt
然后我们定义函数 f(x) 及其导数 f'(x) −
def f(x):
return x**2 - 4*x + 6
def df(x):
return 2*x - 4
F(x) 是需要减少的函数,df 是其导数 (x)。梯度下降法利用导数引导自身趋向最小值,通过沿途显示函数的斜率。
然后定义梯度下降函数。
def gradient_descent(initial_x, learning_rate, num_iterations):
x = initial_x
x_history = [x]
for i in range(num_iterations):
gradient = df(x)
x = x - learning_rate * gradient
x_history.append(x)
return x, x_history
x 的起始值、学习率和所需的迭代次数被发送到梯度下降函数。为了在每次迭代后保存 x 的值,它将 x 初始化为其原始值并生成一个空列表。然后,该方法对提供的迭代次数执行梯度下降,根据方程 x = x - 学习率 * 梯度在每次迭代中更改 x。该函数生成每次迭代的 x 值列表以及 x 的最终值。
现在可以使用梯度下降函数来定位 f(x) 的局部最小值 −
示例
initial_x = 0
learning_rate = 0.1
num_iterations = 50
x, x_history = gradient_descent(initial_x, learning_rate, num_iterations)
print("Local minimum: {:.2f}".format(x))
输出
Local minimum: 2.00
在此示例中,x 在开始时设置为 0,学习率为 0.1,并运行 50 次迭代。最后,我们发布 x 的值,该值应该接近 x=2 处的局部最小值。
绘制函数 f(x) 和每次迭代的 x 值,使我们能够看到梯度下降过程的实际作用 −
示例
# 创建要绘制的 x 值范围
x_vals = np.linspace(-1, 5, 100)
# 绘制函数 f(x)
plt.plot(x_vals, f(x_vals))
# 绘制每次迭代的 x 值
plt.plot(x_history, f(np.array(x_history)), 'rx')
# 标记轴并添加title
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Gradient Descent')
# 显示图
plt.show()
输出
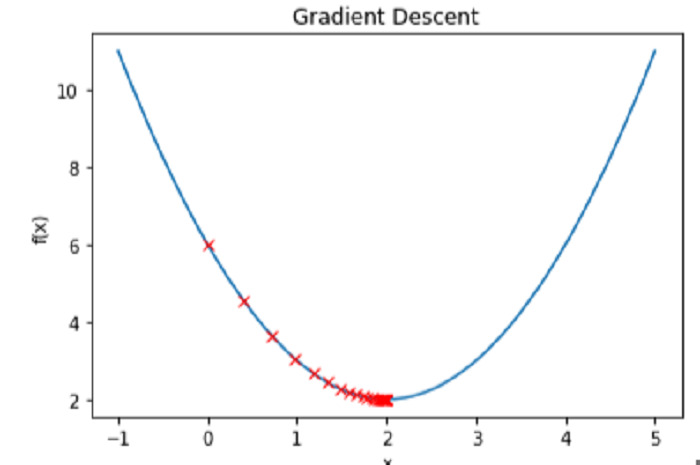
结论
总之,为了找到函数的局部最小值,Python 利用了称为梯度下降的有效优化过程。梯度下降通过计算每一步函数的导数,在最陡峭的下降方向上反复更新输入值,直到达到最低值。在 Python 中实现梯度下降需要指定要优化的函数及其导数,初始化输入值,并确定算法的学习率和迭代次数。优化完成后,可以通过追踪其步骤到最小值并查看其如何达到最小值来评估该方法。梯度下降可以成为机器学习和优化应用中的一项有用技术,因为 Python 可以处理大数据集和复杂的函数。


