Javascript 中的图形数据结构
web developmentfront end technologyjavascript
图形是一组对象的图形表示,其中一些对象对通过链接连接。互连的对象由称为顶点的点表示,连接顶点的链接称为边。
正式来说,图形是一对集合(V, E),其中V是顶点集,E是边集,连接顶点对。请看下面的图表 −
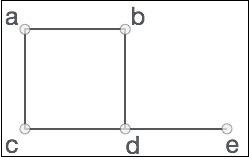
在上图中,
V = {a, b, c, d, e}
E = {ab, ac, bd, cd, de}
术语
数学图形可以在数据结构中表示。我们可以使用顶点数组和二维边数组来表示图形。在继续之前,让我们熟悉一些重要术语 −
顶点 − 图中的每个节点都表示为一个顶点。在下面的示例中,带标签的圆圈表示顶点。因此,A 到 G 是顶点。我们可以使用数组来表示它们,如下图所示。这里 A 可以用索引 0 来标识。B 可以用索引 1 来标识,依此类推。
边 − 边表示两个顶点之间的路径或两个顶点之间的线。在下面的例子中,从 A 到 B、从 B 到 C 等等的线表示边。我们可以使用二维数组来表示数组,如下图所示。这里 AB 可以表示为第 0 行第 1 列的 1,BC 表示为第 1 行第 2 列的 1,依此类推,其他组合保留为 0。
相邻 − 如果两个节点或顶点通过边相互连接,则它们是相邻的。在下面的例子中,B 与 A 相邻,C 与 B 相邻,依此类推。
路径 −路径表示两个顶点之间的边序列。在下面的例子中,ABCD 表示从 A 到 D 的路径。
以下是使用 Javascript 对 Graph 类的完整实现。
示例
const Queue = require("./Queue");
const Stack = require("./Stack");
const PriorityQueue = require("./PriorityQueue");
class Graph {
constructor() {
this.edges = {};
this.nodes = [];
}
addNode(node) {
this.nodes.push(node);
this.edges[node] = [];
}
addEdge(node1, node2, weight = 1) {
this.edges[node1].push({ node: node2, weight: weight });
this.edges[node2].push({ node: node1, weight: weight });
}
addDirectedEdge(node1, node2, weight = 1) {
this.edges[node1].push({ node: node2, weight: weight });
}
// addEdge(node1, node2) {
// this.edges[node1].push(node2);
// this.edges[node2].push(node1);
// }
// addDirectedEdge(node1, node2) {
// this.edges[node1].push(node2);
// }
display() {
let graph = "";
this.nodes.forEach(node => {
graph += node + "->" + this.edges[node].map(n => n.node).join(", ") + "
";
});
console.log(graph);
}
BFS(node) {
let q = new Queue(this.nodes.length);
let explored = new Set();
q.enqueue(node);
explored.add(node);
while (!q.isEmpty()) {
let t = q.dequeue();
console.log(t);
this.edges[t].filter(n => !explored.has(n)).forEach(n => {
explored.add(n);
q.enqueue(n);
});
}
}
DFS(node) {
// 创建一个 Stack 并在其中添加我们的初始节点
let s = new Stack(this.nodes.length);
let explored = new Set();
s.push(node);
// 将第一个节点标记为已探索
explored.add(node);
// 我们将继续,直到我们的 Stack 变空
while (!s.isEmpty()) {
let t = s.pop();
// 记录从 Stack 中出来的每个元素
console.log(t);
// 1. 在 Edges 对象中,我们搜索此节点直接连接到的节点。
// 2. 我们过滤掉已经被探索过的节点。
// 3. 然后我们将每个未探索的节点标记为已探索并将其推送到 Stack。
this.edges[t].filter(n => !explored.has(n)).forEach(n => {
explored.add(n);
s.push(n);
});
}
}
topologicalSortHelper(node, explored, s) {
explored.add(node);
this.edges[node].forEach(n => {
if (!explored.has(n)) {
this.topologicalSortHelper(n, explored, s);
}
});
s.push(node);
}
topologicalSort() {
// 创建一个 Stack 并在其中添加我们的初始节点
let s = new Stack(this.nodes.length);
let explored = new Set();
this.nodes.forEach(node => {
if (!explored.has(node)) {
this.topologicalSortHelper(node, explored, s);
}
});
while (!s.isEmpty()) {
console.log(s.pop());
}
}
BFSShortestPath(n1, n2) {
let q = new Queue(this.nodes.length);
let explored = new Set();
let distances = { n1: 0 };
q.enqueue(n1);
explored.add(n1);
while (!q.isEmpty()) {
let t = q.dequeue();
this.edges[t].filter(n => !explored.has(n)).forEach(n => {
explored.add(n);
distances[n] = distances[t] == undefined ? 1 : distances[t] + 1;
q.enqueue(n);
});
}
return distances[n2];
}
primsMST() {
// 初始化包含 MST 的图
const MST = new Graph();
if (this.nodes.length === 0) {
return MST;
}
// 选择第一个节点作为起始节点
let s = this.nodes[0];
// 创建优先级队列和探索集
let edgeQueue = new PriorityQueue(this.nodes.length * this.nodes.length);
let explored = new Set();
explored.add(s);
MST.addNode(s);
// 以权重为优先级,从此起始节点将所有边添加到 PQ
this.edges[s].forEach(edge => {
edgeQueue.enqueue([s, edge.node], edge.weight);
});
// 取最小边并将其添加到新图中
let currentMinEdge = edgeQueue.dequeue();
while (!edgeQueue.isEmpty()) {
// 继续移除边,直到我们得到一个具有未探索节点的边
while (!edgeQueue.isEmpty() && explored.has(currentMinEdge.data[1])) {
currentMinEdge = edgeQueue.dequeue();
}
let nextNode = currentMinEdge.data[1];
// 再次检查,因为队列可能会变空而不返回未探索的元素
if (!explored.has(nextNode)) {
MST.addNode(nextNode);
MST.addEdge(currentMinEdge.data[0], nextNode, currentMinEdge.priority);
// 再次将所有边添加到 PQ
this.edges[nextNode].forEach(edge => {
edgeQueue.enqueue([nextNode, edge.node], edge.weight);
});
// 将此节点标记为已探索
explored.add(nextNode);
s = nextNode;
}
}
return MST;
}
kruskalsMST() {
// 初始化包含 MST 的图
const MST = new Graph();
this.nodes.forEach(node => MST.addNode(node));
if (this.nodes.length === 0) {
return MST;
}
// 创建优先级队列
let edgeQueue = new PriorityQueue(this.nodes.length * this.nodes.length);
// 将所有边添加到队列:
for (let node in this.edges) {
this.edges[node].forEach(edge => {
edgeQueue.enqueue([node, edge.node], edge.weight);
});
}
let uf = new UnionFind(this.nodes);
// 循环,直到我们探索所有节点或队列为空
while (!edgeQueue.isEmpty()) {
// Get the edge data using destructuring
let nextEdge = edgeQueue.dequeue();
let nodes = nextEdge.data;
let weight = nextEdge.priority;
if (!uf.connected(nodes[0], nodes[1])) {
MST.addEdge(nodes[0], nodes[1], weight);
uf.union(nodes[0], nodes[1]);
}
}
return MST;
}
djikstraAlgorithm(startNode) {
let distances = {};
// 存储对前一个节点的引用
let prev = {};
let pq = new PriorityQueue(this.nodes.length * this.nodes.length);
// 将到所有节点的距离设置为无限,startNode 除外
distances[startNode] = 0;
pq.enqueue(startNode, 0);
this.nodes.forEach(node => {
if (node !== startNode) distances[node] = Infinity;
prev[node] = null;
});
while (!pq.isEmpty()) {
let minNode = pq.dequeue();
let currNode = minNode.data;
let weight = minNode.priority;
this.edges[currNode].forEach(neighbor => {
let alt = distances[currNode] + neighbor.weight;
if (alt < distances[neighbor.node]) {
distances[neighbor.node] = alt;
prev[neighbor.node] = currNode;
pq.enqueue(neighbor.node, distances[neighbor.node]);
}
});
}
return distances;
}
floydWarshallAlgorithm() {
let dist = {};
for (let i = 0; i < this.nodes.length; i++) {
dist[this.nodes[i]] = {};
// 对于现有的边,将 dist 指定为与权重相同
this.edges[this.nodes[i]].forEach(e => (dist[this.nodes[i]][e.node] = e.weight));
this.nodes.forEach(n => {
// 对于所有其他节点,将其分配给无穷大
if (dist[this.nodes[i]][n] == undefined)
dist[this.nodes[i]][n] = Infinity;
// 对于自身边,将 dist 分配给 0
if (this.nodes[i] === n) dist[this.nodes[i]][n] = 0;
});
}
this.nodes.forEach(i => {
this.nodes.forEach(j => {
this.nodes.forEach(k => {
// 检查从 i 到 k 然后从 k 到 j 是否比直接从 i 到 j 更好
// 如果是,则更新
// 将 i 到 j 的值更新为新值
if (dist[i][k] + dist[k][j] < dist[i][j])
dist[i][j] = dist[i][k] + dist[k][j];
});
});
});
return dist;
}
}
class UnionFind {
constructor(elements) {
// 断开连接的组件数
this.count = elements.length;
// 跟踪连接的组件
this.parent = {};
// 初始化数据结构,使所有元素都以自己为父元素
elements.forEach(e => (this.parent[e] = e));
}
union(a, b) {
let rootA = this.find(a);
let rootB = this.find(b);
// 根元素相同,因此它们已连接。
if (rootA === rootB) return;
// 始终将根元素较小的元素作为父元素。
if (rootA < rootB) {
if (this.parent[b] != b) this.union(this.parent[b], a);
this.parent[b] = this.parent[a];
} else {
if (this.parent[a] != a) this.union(this.parent[a], b);
this.parent[a] = this.parent[b];
}
}
// Returns final parent of a node
find(a) {
while (this.parent[a] !== a) {
a = this.parent[a];
}
return a;
}
// 检查两个节点的连通性
connected(a, b) {
return this.find(a) === this.find(b);
}
}


