由最多 M 个值为 K 的连续节点组成的根到叶路径的计数
简介
二叉树是一种迷人的数据结构,在计算机科学和编程中有着广泛的应用。一个有趣的问题是从给定的由父节点及其子节点组成的树中找到计数。二叉树由节点组成,根节点已确定,子节点可根据用户需要从中给出。K 值已确定,遍历方式由 M 值选择。
根到叶路径的计数
该图由各种节点创建,这些节点以整数形式保存值。本文主要介绍如何从起始节点(根节点)到叶子节点(子节点)的计数。
示例
该图由具有各种节点的二叉树创建。
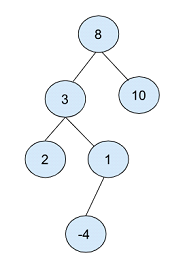
在上面的二叉树中,根节点选择为"8"。
然后创建两个节点,一个值为 3,另一个值为 10,分别占据根节点的左侧和右侧位置。
以值为 2 的节点为根,创建另一个子节点,其左侧和右侧值分别为 2 和 1。
最后,值为 1 的子节点创建一个值为 -4 的子节点。
方法 1:使用递归函数计算由最多 M 个连续节点组成的从根到叶的路径的 C++ 代码,这些路径的值均为 K
为了有效地解决这个问题,我们将利用树遍历算法和递归等基本概念。
算法
步骤 1:创建一个用于表示树节点的结构,该结构包含两个指针(左子节点和右子节点)以及用于存储节点值的整数字段。
步骤 2:设计一个递归函数,从根开始遍历二叉树,同时跟踪当前路径长度(初始化为 0)、连续出现次数(初始设置为 0)、目标值 K、允许的最大连续出现次数 M。
步骤 3:在每个左子树和右子树上递归调用该函数,传递更新的参数,例如递增的路径长度和连续出现次数(如果适用)。
步骤 4:对于遍历期间访问的每个非空节点:
a) 如果其值等于 K,则将两个变量都加一。
b) 如果其值与 K 不匹配或超过路径中迄今为止已经遇到的 M 个连续出现次数,则将变量重置回零。
步骤 5:在遍历树时,如果子节点在左侧和右侧两种情况下的值均为零 - 我们可以用两种方式处理,即
a) 检查变量是否不超过 M。
b) 如果是,则从开始到结束增加路径总数,满足条件。
示例
//在一个标头中包含所有内容
#include<bits/stdc++.h>
using namespace std;
//创建具有两个指针的结构,分别为 up 和 down
struct Vertex {
int data;
struct Vertex* up;
struct Vertex* down;
};
//countPaths 函数声明有五个参数;根 = 结束;节点 = 顶点;左 = 上;右 = 下
int countPaths(Vertex* end, int K, int M, int currCount, int
consCount) {
//检查根是否等于 1 且大于最大值,值增加
if (end == NULL || consCount > M) {
return 0;
}
//检查根是否等于 K 值,增加 1
if (end->data == K) {
currCount++;
consCount++;
} else {
//如果不相等,则返回 0
currCount = 0;
}
if (end->up == NULL && end->down == NULL) {
if (currCount <= M) {
return 1;
} else {
return 0;
}
}
return countPaths(end->up, K, M, currCount, consCount) + countPaths(end->down, K, M, currCount, consCount);
}
//主函数用于测试实现
int main() {
Vertex* end = new Vertex();
end->data = 8;
end->up = new Vertex();
end->up->data = 3;
end->down = new Vertex();
end->down->data = 10;
end->up->up = new Vertex();
end->up->up->data = 2;
end->up->down = new Vertex();
end->up->down->data = 1;
end->up->down->up = new Vertex();
end->up->down->up->data = -4;
int K = 1; // 节点的值
int M = 2; // 最大连续节点数
int currCount = -1; // 当前计数
int consCount = -1; // 连续计数
cout << "从给定的" << M << "节点图中获取的路径数,其值为 " << K << ",为 " << " << countPaths(end, K, M, currCount, consCount) << endl;
return 0;
}
输出
从给定的 2 个节点图中获取的路径数,其值为 1,为 3
结论
在本文中,我们探讨了从顶部(即叶子)到末端(即根)计算路径数的问题。通过使用 C++ 中的树遍历算法和递归技术,可以有效地解决此类问题。遍历二叉树的过程看似困难,但通过示例,它变得简单。


