HTML CSS JAVASCRIPT BOOTSTRAP JQUERY PHP SQL PYTHON PYTHON2 JAVA C C++ C# Linux AI 教程库 参考手册 测验 练习 HOWTO FAQ
❮ 上一节 下一节 ❯

Keras - 卷积神经网络

让我们将模型从 MPL 修改为 卷积神经网络 (CNN)，以解决我们之前的数字识别问题。

CNN 可以表示为以下 −

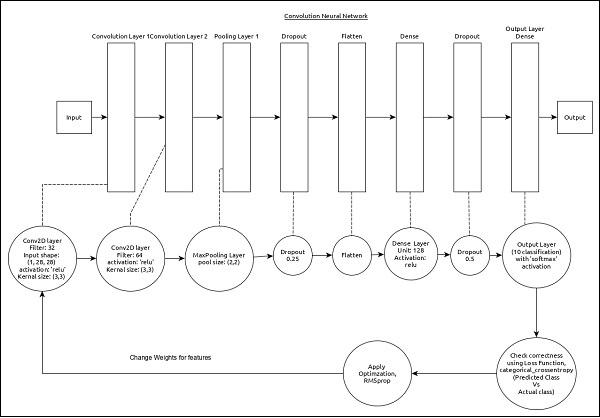
卷积神经网络

该模型的核心特征如下 −

  • 输入层由 (1, 8, 28) 个值组成。

  • 第一层，Conv2D 由 32 个过滤器和内核大小为 (3,3) 的"relu"激活函数组成。

  • 第二层，Conv2D 由 64 个过滤器组成和"relu"激活函数，其内核大小为 (3,3)。

  • 第三层，MaxPooling，池大小为 (2, 2)。

  • 第五层，Flatten，用于将其所有输入展平为一维。

  • 第六层，Dense，由 128 个神经元和"relu"激活函数组成。

  • 第七层，Dropout，其值为 0.5。

  • 第八层也是最后一层，由 10 个神经元和"softmax"激活函数组成。

  • 使用 categorical_crossentropy 作为损失函数。

  • 使用 Adadelta() 作为优化器。

  • 使用 accuracy 作为指标。

  • 使用 128 作为批次大小。

  • 使用 20 作为时期。

步骤 1 − 导入模块

让我们导入必要的模块。

import keras 
from keras.datasets import mnist 
from keras.models import Sequential 
from keras.layers import Dense, Dropout, Flatten 
from keras.layers import Conv2D, MaxPooling2D 
from keras import backend as K 
import numpy as np

步骤 2 − 加载数据

让我们导入 mnist 数据集。

(x_train, y_train), (x_test, y_test) = mnist.load_data()

步骤 3 − 处理数据

让我们根据我们的模型更改数据集，以便将其输入到我们的模型中。

img_rows, img_cols = 28, 28 

if K.image_data_format() == 'channels_first': 
   x_train = x_train.reshape(x_train.shape[0], 1, img_rows, img_cols) 
   x_test = x_test.reshape(x_test.shape[0], 1, img_rows, img_cols) 
   input_shape = (1, img_rows, img_cols) 
else: 
   x_train = x_train.reshape(x_train.shape[0], img_rows, img_cols, 1) 
   x_test = x_test.reshape(x_test.shape[0], img_rows, img_cols, 1) 
   input_shape = (img_rows, img_cols, 1) 
   
x_train = x_train.astype('float32') 
x_test = x_test.astype('float32') 
x_train /= 255 
x_test /= 255 

y_train = keras.utils.to_categorical(y_train, 10) 
y_test = keras.utils.to_categorical(y_test, 10)

除了输入数据的形状和图像格式配置外，数据处理与 MPL 模型类似。

步骤 4 −创建模型

让我们创建实际的模型。

model = Sequential()
model.add(Conv2D(32, kernel_size = (3, 3),
	activation = 'relu', input_shape = input_shape))
model.add(Conv2D(64, (3, 3),activation = 'relu'))
model.add(MaxPooling2D(pool_size = (2, 2)))
model.add(Dropout(0.25)) model.add(Flatten())
model.add(Dense(128,activation = 'relu'))
model.add(Dropout(0.5))
model.add(Dense(10,activation = 'softmax'))

步骤 5 −编译模型

让我们使用选定的损失函数、优化器和指标来编译模型。

model.compile(loss = keras.losses.categorical_crossentropy,
	optimizer = keras.optimizers.Adadelta(), metrics = ['accuracy'])

步骤 6 − 训练模型

让我们使用 fit() 方法训练模型。

model.fit(
   x_train, y_train, 
   batch_size = 128, 
   epochs = 12, 
   verbose = 1, 
   validation_data = (x_test, y_test)
)

执行应用程序将输出以下信息 −

Train on 60000 samples, validate on 10000 samples Epoch 1/12 
60000/60000 [==============================] - 84s 1ms/step - loss: 0.2687 
- acc: 0.9173 - val_loss: 0.0549 - val_acc: 0.9827 Epoch 2/12 
60000/60000 [==============================] - 86s 1ms/step - loss: 0.0899 
- acc: 0.9737 - val_loss: 0.0452 - val_acc: 0.9845 Epoch 3/12 
60000/60000 [==============================] - 83s 1ms/step - loss: 0.0666 
- acc: 0.9804 - val_loss: 0.0362 - val_acc: 0.9879 Epoch 4/12 
60000/60000 [==============================] - 81s 1ms/step - loss: 0.0564 
- acc: 0.9830 - val_loss: 0.0336 - val_acc: 0.9890 Epoch 5/12 
60000/60000 [==============================] - 86s 1ms/step - loss: 0.0472 
- acc: 0.9861 - val_loss: 0.0312 - val_acc: 0.9901 Epoch 6/12 
60000/60000 [==============================] - 83s 1ms/step - loss: 0.0414 
- acc: 0.9877 - val_loss: 0.0306 - val_acc: 0.9902 Epoch 7/12 
60000/60000 [==============================] - 89s 1ms/step - loss: 0.0375 
-acc: 0.9883 - val_loss: 0.0281 - val_acc: 0.9906 Epoch 8/12 
60000/60000 [==============================] - 91s 2ms/step - loss: 0.0339 
- acc: 0.9893 - val_loss: 0.0280 - val_acc: 0.9912 Epoch 9/12 
60000/60000 [==============================] - 89s 1ms/step - loss: 0.0325 
- acc: 0.9901 - val_loss: 0.0260 - val_acc: 0.9909 Epoch 10/12 
60000/60000 [==============================] - 89s 1ms/step - loss: 0.0284 
- acc: 0.9910 - val_loss: 0.0250 - val_acc: 0.9919 Epoch 11/12 
60000/60000 [==============================] - 86s 1ms/step - loss: 0.0287 
- acc: 0.9907 - val_loss: 0.0264 - val_acc: 0.9916 Epoch 12/12 
60000/60000 [==============================] - 86s 1ms/step - loss: 0.0265 
- acc: 0.9920 - val_loss: 0.0249 - val_acc: 0.9922

步骤 7 − 评估模型

让我们使用测试数据评估模型。

score = model.evaluate(x_test, y_test, verbose = 0)

print('测试损失：', score[0])
print('测试准确率：', score[1])

执行上述代码将输出以下信息 −

测试损失：0.024936060590433316
测试准确率：0.9922

测试准确率为 99.22%。我们已经创建了一个最佳模型来识别手写数字。

步骤 8 −预测

最后，从图像中预测数字，如下所示 −

pred = model.predict(x_test)
pred = np.argmax(pred, axis = 1)[:5]
label = np.argmax(y_test,axis = 1)[:5]

print(pred)
print(label)

上述应用程序的输出如下 −

[7 2 1 0 4]
[7 2 1 0 4]

两个数组的输出相同，表明我们的模型正确预测了前五张图像。

❮ 上一节 下一节 ❯