C++ 删除长度 < K 的从根到叶路径上的节点
给定一棵树,我们需要删除长度小于给定 k 的路径的叶节点。
输入 −
K = 4。
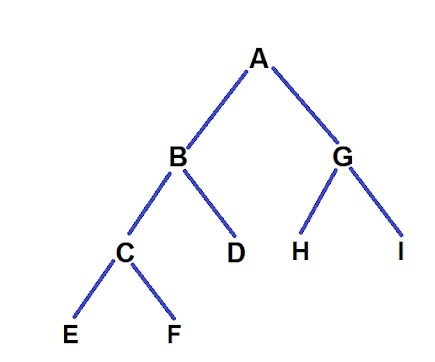
输出 −
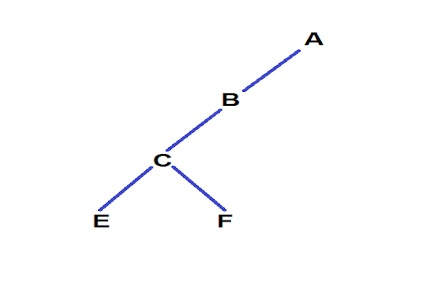
解释
The paths were : 1. A -> B -> C -> E length = 4 2. A -> B -> C -> F length = 4 3. A -> B -> D length = 3 4. A -> G -> H length = 3 5. A -> B -> I length = 3 现在,如您所见,路径 3、4、5 的长度为 3,小于给定的 k,因此我们删除这些路径的叶节点,即 D、H、I。 现在对于路径 4 和 5,当删除 H 和 I 时,我们注意到现在 G 也是一个路径长度为 2 的叶节点,因此我们再次删除节点 G,程序到此结束。
我们将以后序格式遍历树;然后,我们创建一个递归函数,如果叶节点的路径长度小于 K,则删除它们。
寻找解决方案的方法
在这种方法中,我们现在以后序遍历的方式进行遍历;我们尝试递归地删除路径长度小于 k 的叶节点并继续这样做。
示例
上述方法的 C++ 代码
#include<bits/stdc++.h>
using namespace std;
struct Node{ // 我们节点的结构
char data;
Node *left, *right;
};
Node *newNode(int data){ // 插入新节点
Node *node = new Node;
node->data = data;
node->left = node->right = NULL;
return node;
}
Node *trimmer(Node *root, int len, int k){
if (!root) // 如果 root == NULL,则返回
return NULL;
root -> left = trimmer(root -> left, len + 1, k); // 遍历左阶段
root -> right = trimmer(root -> right, len + 1, k); // 遍历右阶段
if (!root -> left && !root -> right && len < k){
delete root;
return NULL;
}
return root;
}
Node *trim(Node *root, int k){
return trimmer(root, 1, k);
}
void printInorder(Node *root){
if (root){
printInorder(root->left);
cout << root->data << " ";
printInorder(root->right);
}
}
int main(){
int k = 4;
Node *root = newNode('A');
root->left = newNode('B');
root->right = newNode('G');
root->left->left = newNode('C');
root->left->right = newNode('D');
root->left->left->left = newNode('E');
root->left->left->right = newNode('F');
root->right->left = newNode('H');
root->right->right = newNode('I');
printInorder(root);
cout << "\n";
root = trim(root, k);
printInorder(root);
return 0;
}
输出
E C F B D A H G I E C F B A
Explanation of the Above Code
In this code, we are using a recursive function that is traversing our tree and keeping the stats of the left and right subtrees. Now we arrive at a leaf node; we check the path length till that node. If the path length is less, then we delete this node, and then we return NULL; otherwise, the code continues.
Conclusion
In this tutorial, we solve a problem to Remove nodes on the root to leaf paths of length < K using recursion. We also learned the C++ program and recursion for this problem and the complete approach we solved. We can write the same program in other languages such as C, java, python, and other languages. We hope you find this tutorial helpful.

