C++ 查询树中子树的 DFS
c++server side programmingprogramming
在这个问题中,我们给定一个二叉树,我们需要从一个特定节点执行 dfs,其中我们假设给定节点为根并从它执行 dfs。
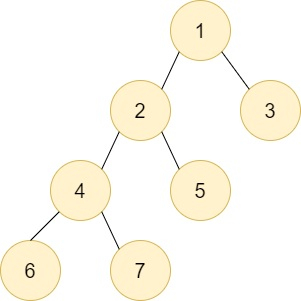
在上面的树中,假设我们需要从节点 F 执行 DFS
在本教程中,我们将应用一些非正统方法,以便大大降低我们的时间复杂度,因此我们也能够在更高的约束条件下运行此代码。
方法 −在这种方法中,我们不会简单地采用幼稚的方法,即简单地对每个节点应用 dfs,因为它不适用于更高的约束,所以我们尝试使用一些非常规方法来避免获得 TLE。
#include <bits/stdc++.h>
using namespace std;
#define N 100000
// 邻接列表用于存储
// 树节点连接
vector<int> v[N];
unordered_map<int, int> mape; // 将用于将节点与其索引关联
vector<int> a;
void dfs(int nodesunder[], int child, int parent){// 用于 dfs 和 的函数预先计算我们的 nodesunder
a.push_back(child); // 存储我们的树的 dfs
// 子子树的 nodesunder
nodesunder[child] = 1;
for (auto it : v[child]) { // 执行正常 dfs
if (it != parent) { // 因为子节点可以爬上去
// 它是父节点,所以我们试图避免这种情况,因为它会变成一个循环
dfs(nodesunder, it, child); // 递归调用
nodesunder[child] += nodesunder[it]; // 存储增加的 nodesunder
// 按其子节点下的节点数
}
}
}
// 打印节点子树的 DFS 的函数
void printDFS(int node, int nodesunder[]){
int ind = mape[node]; // dfs 数组中节点的索引
cout << "子树的 DFS << node << ": ";
// 打印子树的 DFS
for (int i = ind; i < ind + nodesunder[node]; i++){ // 遍历 dfs 数组然后
// 打印给定节点下的所有节点
cout << a[i] << &" &";;
}
cout << endl;
}
void addEdgetoGraph(int x, int y){ // 用于维护邻接列表
v[x].push_back(y);
v[y].push_back(x);
}
void mark(){ // 用 dfs 数组中的索引标记每个节点
int size = a.size();
// 标记索引
for (int i = 0; i < size; i++) {
mape[a[i]] = i;
}
}
int main(){
int n = 7;
// 添加树的边
addEdgetoGraph(1, 2);
addEdgetoGraph(1, 3);
addEdgetoGraph(2, 4);
addEdgetoGraph(2, 5);
addEdgetoGraph(4, 6);
addEdgetoGraph(4, 7);
// 用于存储子树下存在的节点的数组
// 树中每个节点的子树下节点
int nodesunder[n + 1];
dfs(nodesunder, 1, 0); // 生成我们的 nodesunder 数组
mark(); // 标记图中的索引
// 查询 1
printDFS(2, nodesunder);
// 查询 2
printDFS(4, nodesunder);
return 0;
}
输出
子树 2 的 DFS:2 4 6 7 5 子树 4 的 DFS:4 6 7
理解代码
在这种方法中,我们预先计算 dfs 的顺序并将其存储在一个向量中,现在当我们预先计算了 dfs 时,我们还从每个节点开始计算每个子树下存在的节点,然后我们简单地从该节点的起始索引遍历到其子树内存在的所有节点数。
结论
在本教程中,我们解决了一个问题,以解决树中子树的 DFS 查询。我们还学习了针对此问题的 C++ 程序以及解决此问题的完整方法(常规)。
我们可以用其他语言(如 C、java、python 和其他语言)编写相同的程序。希望您觉得本文有用。


