C++ 瓦里尼翁平行四边形的周长和面积
瓦里尼翁平行四边形由四边形各边的中点连接而成。 假设我们有一个四边形 ABCD。每条边的中点分别为 P、Q、R 和 S。如果我们连接所有中点,它将始终形成一个平行四边形 PQRS,称为 Varignon 平行四边形。
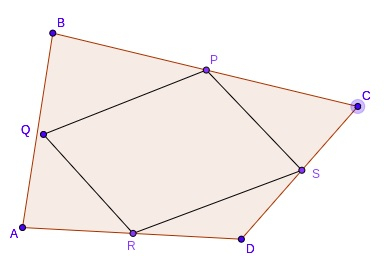
在本教程中,我们将讨论如何根据给定的两条对角线和四边形的面积(例如 −)来找到 Varignon 平行四边形的周长和面积。
输入:d1 = 6,d2 = 9,面积 = 12 输出: 周长 = 15 面积 = 6 输入:d1 = 11, d2 = 13,面积 = 32 输出: 周长 = 24 面积 = 16
求解方法
三角形 P 和 Q 分别是 AB、AC 的中点,
根据中点定理,PQ = (1/2)*AC
类似地将定理应用于三角形 ADC,RS = (1/2)*BD,
因此 PQ=RS=(1/2)*AC 且 PS=QR=(1/2)*BD
PQRS 的周长 = AC + BD(对角线之和)
EF=GH=(1/2)*AC 且 EH=FG=(1/2)*BD
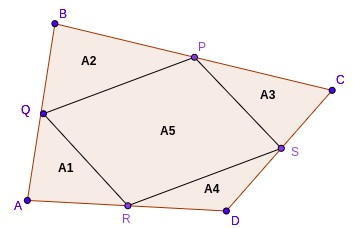
对于 PQRS 的面积,我们将图形分成四个三角形,四个三角形的面积为,
A1=(1/4)*BAD 的面积
类似地,A2=(1/4)*ABC 的面积
A3=(1/4)*BCD 的面积
A4=(1/4)*ACD 的面积。
A1 + A2 + A3 + A4 = (1/4)*(三角形 ACD+ABC+BCD+BAD 的面积)
= (¼) * 2* ABCD 面积
= (½) * 四边形 ABCD 面积
现在 A1 + A2 + A3 + A4 = (½) * 四边形 ABCD 面积
这意味着 A5 = (½) * 四边形 ABCD 面积
所以平行四边形 PQRS 面积 = (½) * 四边形 ABCD 面积
现在我们只需使用 C++ 应用公式即可找到 PQRS 的周长和面积。
示例
上述方法的 C++ 代码
#include <bits/stdc++.h>
using namespace std;
int main(){
float d1 = 6, d2 = 9, area_ABCD = 12;
float area_PQRS = area_ABCD/2;
float perimeter = d1 + d2;
cout << "Area of parallelogram PQRS = " << area_PQRS << " and perimeter = " << perimeter;
return 0;
}
输出
Area of parallelogram PQRS = 6 and perimeter = 15
结论
在本教程中,我们讨论了 Varignon 的平行四边形以及如何找到面积和周长。我们讨论了使用中点定理推导平行四边形的周长和面积。我们还讨论了可以使用 C、Java、Python 等编程语言来解决此问题的 C++ 程序。希望本教程对您有所帮助。


