时间序列 - 移动平均线
对于固定时间序列,移动平均模型将变量在时间"t"处的值视为其之前"q"时间步长的残差的线性函数。 残差是通过将时间"t"的值与之前值的移动平均值进行比较来计算的。
数学上可以写成 −
$$y_{t} = c\:+\:\epsilon_{t}\:+\:\theta_{1}\:\epsilon_{t-1}\:+\:\theta_{2}\:\epsilon_{t-2}\:+\:...+:\theta_{q}\:\epsilon_{t-q}\:$$
其中'q'是移动平均趋势参数
$\epsilon_{t}$ 是白噪声,并且
$\epsilon_{t-1}, \epsilon_{t-2}...\epsilon_{t-q}$ 是之前时间段的误差项。
"q"的值可以使用各种方法进行校准。 找到"q"的合适值的一种方法是绘制部分自相关图。
部分自相关图显示了变量在先前时间步长与自身之间的关系,去除了间接相关,这与显示直接相关和间接相关的自相关图不同,让我们看看我们的"温度"变量的样子 数据。
Showing PACP
In [143]:
from statsmodels.graphics.tsaplots import plot_pacf plot_pacf(train, lags = 100) plt.show()
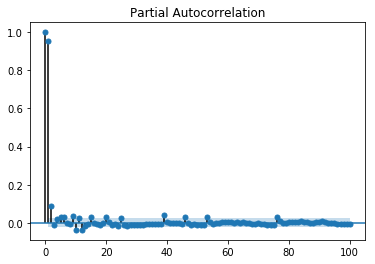
以与相关图相同的方式读取部分自相关。

