使用 C 的 DSA - 堆栈

概述

堆栈是一种数据结构，它只允许在一端对数据进行操作。它只允许访问最后插入的数据。堆栈也称为 LIFO（后进先出）数据结构，推送和弹出操作以这样的方式相关：只有最后推送（添加到堆栈）的项目才能弹出（从堆栈中删除）。

堆栈表示

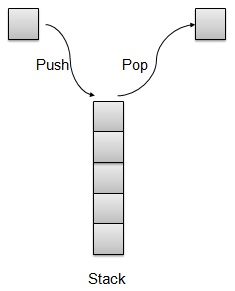
我们将在本文中使用数组实现堆栈。

基本操作

以下是堆栈的两个主要操作。

• 推送 −将元素推送到堆栈顶部。

• Pop − 从堆栈顶部弹出一个元素。

堆栈支持以下几个操作。

• Peek − 获取堆栈顶部元素。

• isFull − 检查堆栈是否已满。

• isEmpty − 检查堆栈是否为空。

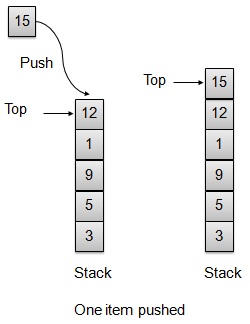
推送操作

每当将元素推送到堆栈时，堆栈都会将该元素存储在存储顶部并增加顶部索引以供以后使用。如果存储已满，通常会显示错误消息。

// Operation : Push
// push item on the top of the stack 
void push(int data) {
   if(!isFull()){
      // increment top by 1 and insert data 
      intArray[++top] = data;
   } else {
      printf("Cannot add data. Stack is full.
");
   }      
}

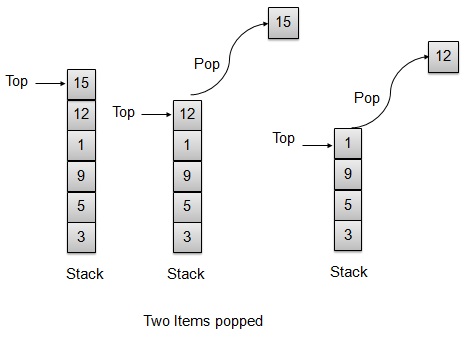
弹出操作

每当要从堆栈中弹出一个元素时，堆栈都会从存储顶部检索该元素并减少顶部索引以供以后使用。

// Operation : Pop
// pop item from the top of the stack 
int pop() {
   //retrieve data and decrement the top by 1
   return intArray[top--];        
}

示例

StackDemo.c

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>

// size of the stack
int size = 8;       

// stack storage
int intArray[8];     

// top of the stack
int top = -1;            

// Operation : Pop
// pop item from the top of the stack 
int pop() {
   //retrieve data and decrement the top by 1
   return intArray[top--];        
}
// Operation : Peek
// view the data at top of the stack 
int peek() {       
   //retrieve data from the top
   return intArray[top];
}
//Operation : isFull
//return true if stack is full 
bool isFull(){
   return (top == size-1);
}

// Operation : isEmpty
// return true if stack is empty 
bool isEmpty(){
   return (top == -1);
}
// Operation : Push
// push item on the top of the stack 
void push(int data) {
   if(!isFull()){
      // increment top by 1 and insert data 
      intArray[++top] = data;
   } else {
      printf("Cannot add data. Stack is full.
");
   }      
}
main() {
   // push items on to the stack 
   push(3);
   push(5);
   push(9);
   push(1);
   push(12);
   push(15);

   printf("Element at top of the stack: %d
" ,peek());
   printf("Elements: 
");

   // print stack data 
   while(!isEmpty()){
      int data = pop();
      printf("%d
",data);
   }
   printf("Stack full: %s
" , isFull()?"true":"false");
   printf("Stack empty: %s
" , isEmpty()?"true":"false");
}

输出

如果我们编译并运行上述程序，则会产生以下输出 −

Element at top of the stack: 15
Elements: 
15
12
1
9
5
3
Stack full: false
Stack empty: true