奇异值分解

pythonnumpymachine learning

机器学习使用奇异值分解的数学方法来理解庞大而复杂的数据集。

在这种数学方法中，一个唯一值矩阵 A 通过分解被分解为三个矩阵。就 A 的分量而言，矩阵 A 的奇异值分解可以写为 A=UDVT。在这种情况下，S 表示 A 的奇异值，而 U 和 V 分别代表 A 的左和右奇异向量。

数学算法

给定矩阵 A，找到矩阵 A 的转置，即 (AT)。
查找 A*AT
查找 A*AT 的特征向量
使用公式 A*AT - λ I = 0 查找特征向量，其中 I 是 A 的等阶单位矩阵。
计算 A 的奇异值为 ATA 特征值的平方根。奇异值按降序排列。
我们计算 A 的左和右奇异向量 −
- 对于每个奇异值，找到 AT A 的对应特征向量。
- 每个特征向量都经过归一化以具有单位长度。
- A 的左奇异向量是 A AT 对应于 A 的非零奇异值的特征向量。
- A 的右奇异向量是 AT A 的归一化特征向量。
按降序排列的 A 的奇异值由 S 的对角线项表示。

A 的左奇异向量由U 的列

V 的列表示 A 的右奇异向量。

示例 1

以下示例对数据集执行 SVD 并将其绘制为散点图。从 UCI 数据集加载数据集，并根据参数对数据进行分离。数据被标准化，并且.svd()应用于数据，它是Numpy的linalg(线性代数)模块的一部分。散点图用于绘制数据。

算法

步骤1 - 导入Pandas，Numpy和Matplotlib库。
步骤2 - 将数据集的链接存储在url变量中。
步骤3 - 将特征(即数据集的列名)存储在名为names的数组中。
步骤4 - 使用pd.read_csv()方法读取数据
步骤5 - 将特征与目标
步骤 6 - 使用公式 (X - Xmean) / 标准差 X 对特征进行标准化
步骤 7 - 使用 Numpy 的 linalg 模块的 .svd() 方法对 X 执行 SVD
步骤 8 - 构造对角矩阵 S
步骤 9 - 使用 Matplotlib 的 .scatter() 方法绘制 U
步骤 10 - 运行代码后，可以在弹出窗口中看到散点图

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt


url='https://archive.ics.uci.edu/ml/machine-learning-databases/abalone/abalone.data'
names = ['Length', 'Diam', 'Height', 'Whole']
abalone = pd.read_csv(url, names=names)

X = abalone.iloc[:, :-1].values
y = abalone.iloc[:, -1].values

X = (X - X.mean(axis=0)) / X.std(axis=0)

U, s, Vt = np.linalg.svd(X, full_matrices=False)

S = np.diag(s)

plt.scatter(U[:, 0], U[:, 1], c=y)
plt.xlabel('X')
plt.ylabel('Y')
plt.show()

输出

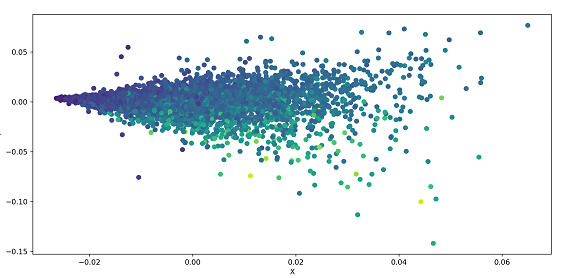
示例 2

在下面的示例中，我们计算作为参数传递给函数的矩阵 A 的 SVD。我们计算特征向量和特征值并按降序排列。该函数返回右奇异矩阵的特征向量、奇异值和转置。

算法

步骤 1 - 导入 numpy 库
步骤 2 - 定义一个以矩阵 A 作为输入的函数 svd
步骤 3 - 使用 Numpy 的 linalg 方法的 .eigh() 方法计算 A^T * A 的特征值和特征向量。
步骤 4 - 特征向量和特征值按降序排列。
步骤 5 - 计算A
步骤 6 - 函数返回特征向量、奇异值和右奇异矩阵的转置。
步骤 7 - 将值存储在数组 A 中并以 A 作为参数调用函数 svd
步骤 8 - 将函数返回的值分别存储在 U、S、V 中并打印它们

import numpy as np
def svd(A):
   eigen_values, eigen_vectors = np.linalg.eigh(np.dot(A.T, A))
   
 
   sorted_indices = eigen_values.argsort()[::-1]
   eigen_values = eigen_values[sorted_indices]
   eigen_vectors = eigen_vectors[:,sorted_indices]
   
   singular_values = np.sqrt(eigen_values)
   right_singular_vectors = np.dot(A, eigen_vectors)
   right_singular_vectors /= singular_values
   
   return eigen_vectors, singular_values, right_singular_vectors.T
A = np.array([[1, 2, 2], [4, 5, 9], [7, 8, 10]])
U, S, V = svd(A)
print (U)
print (S)
print (V)

在上面的代码中，svd() 函数以矩阵为输入，计算矩阵的特征值和特征向量。我们对计算出的特征值和特征向量按降序排序，并通过对特征值取平方根来计算奇异值，并将其存储在数组中。

然后，我们通过将矩阵与排序后的特征向量相乘，并将结果除以之前计算出的奇异值来计算右奇异向量。因此，该函数返回特征向量、奇异值和右奇异向量的转置。

Output

[[-0.43649583 -0.55427262 -0.70869828]
 [-0.52004753 -0.48734746  0.70145778]
 [-0.73418115  0.67474019 -0.07552297]]

[18.45494908  1.76319494  0.5531709 ]

[[-0.15957525 -0.59354546 -0.7888216 ]
 [-0.10179655  0.80469488 -0.58489624]
 [ 0.98192322 -0.01303565 -0.18883027]]