Python 中的局部加权线性回归
局部加权线性回归是一种非参数方法/算法。在线性回归中,数据应呈线性分布,而局部加权回归适用于非线性分布的数据。通常,在局部加权回归中,距离查询点较近的点比距离查询点较远的点具有更大的权重。
参数和非参数模型
参数
参数模型是将函数简化为已知形式的模型。它具有一组参数,可通过这些参数汇总数据。
这些参数的数量是固定的,这意味着模型已经知道这些参数,并且它们不依赖于数据。它们在本质上也与训练样本无关。
例如,让我们有一个如下所述的映射函数。
b0+b1x1+b2x2=0
从等式中,b0、b1 和 b2 是控制截距和斜率的线的系数。输入变量由 x1 和 x2 表示。
非参数
非参数算法不对映射函数的类型做出特定假设。这些算法不接受输入和输出数据之间的映射函数的特定形式为真。
它们可以自由地从训练数据中选择任何函数形式。因此,参数模型估计映射函数所需的数据比参数模型多得多。
成本函数和权重的推导
线性回归的成本函数是
$$\mathrm{\displaystyle\sum\limits_{i=1}^m (y^{{(i)}} \:-\:\Theta^Tx)^2}$$
在局部加权线性回归的情况下,成本函数被修改为
$$\mathrm{\displaystyle\sum\limits_{i=1}^m w^i(w^{{(i)}} \:-\:\Theta^Tx)^2}$$
其中 𝑤(𝑖) 表示第 i 个训练样本的权重。
加权函数可以定义为
$$\mathrm{w(i)\:=\:exp\:(-\frac{x^i-x^2}{2\tau^2})}$$
x 是我们想要进行预测的点。x(i) 是第 i 个训练示例
τ 可以称为权重函数的高斯钟形曲线的带宽。
可以根据与查询点的距离调整 τ 的值以改变 w 的值。
τ 的值越小,数据点到查询点的距离越小,w 的值越大(权重越大),反之亦然。
w 的值通常在 0 到 1 之间。
局部加权回归算法没有训练阶段。所有权重 𝜃 均在预测阶段确定。
示例
我们考虑一个由以下点组成的数据集:
2,5,10,17,26,37,50,65,82
取查询点 x = 7 和数据集中的三个点 5,10,26
因此 x(1) = 5, x(2) = 10 , x(3) = 26 。让 𝜏 = 0.5
因此,
$$\mathrm{w(1) = exp( - ( 5 – 7 )^2 / 2 x 0.5^2) = 0.00061}$$
$$\mathrm{w(2) = exp( - (9 – 7 )^2 / 2 x 0.5^2) = 5.92196849e-8}$$
$$\mathrm{w(3) = exp( - (26 – 7 )^2 / 2 x 0.5^2) = 1.24619e-290}$$
$$\mathrm{J(\Theta) = = 0.00061 * (\Theta^ T x(1) – y(1) ) + 5.92196849e-8 * (\Theta^ T x(2) – y(2) ) + 1.24619e-290 *( \Theta^ T x(3) – y(3) )}$$
从以上示例可以看出,查询点 (x) 越接近特定数据点/样本 x(1),x(2),x(3) 等,w 的值就越大。对于远离查询点的数据点,权重会呈指数下降。
随着 x(i) 和 x 之间的距离增加,权重会减小。这会降低误差项对成本函数的贡献,反之亦然。
Python 中的实现
以下代码片段演示了局部加权线性回归算法。
示例
import pandas as pd import numpy as np import matplotlib.pyplot as plt %matplotlib inline df = pd.read_csv('/content/tips.csv') features = np.array(df.total_bill) labels = np.array(df.tip) def kernel(data, point, xmat, k): m,n = np.shape(xmat) ws = np.mat(np.eye((m))) for j in range(m): diff = point - data[j] ws[j,j] = np.exp(diff*diff.T/(-2.0*k**2)) return ws def local_weight(data, point, xmat, ymat, k): wei = kernel(data, point, xmat, k) return (data.T*(wei*data)).I*(data.T*(wei*ymat.T)) def local_weight_regression(xmat, ymat, k): m,n = np.shape(xmat) ypred = np.zeros(m) for i in range(m): ypred[i] = xmat[i]*local_weight(xmat, xmat[i],xmat,ymat,k) return ypred m = features.shape[0] mtip = np.mat(labels) data = np.hstack((np.ones((m, 1)), np.mat(features).T)) ypred = local_weight_regression(data, mtip, 0.5) indices = data[:,1].argsort(0) xsort = data[indices][:,0] fig = plt.figure() ax = fig.add_subplot(1,1,1) ax.scatter(features, labels, color='blue') ax.plot(xsort[:,1],ypred[indices], color = 'red', linewidth=3) plt.xlabel('Total bill') plt.ylabel('Tip') plt.show()
输出
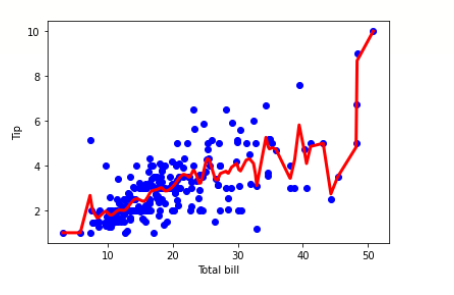
何时可以使用局部加权线性回归?
当特征数量较少时。
当不需要特征选择时
局部加权线性回归的优势。
在局部加权线性回归中,局部权重是根据每个数据点计算的,因此出现大错误的可能性较小。
我们拟合一条曲线,结果错误被最小化。
在这个算法中,有许多小的局部函数,而不是一个要最小化的全局函数。局部函数在调整变化和误差方面更有效。
局部加权线性回归的缺点。
这个过程非常详尽,可能会消耗大量资源。
对于更简单的线性相关问题,我们可以简单地避免使用局部加权算法。
无法容纳大量特征。
结论
因此,简而言之,局部加权线性回归更适合于数据呈非线性分布,并且我们仍希望使用回归模型拟合数据而不影响预测质量的情况。


