如何解读时间序列的 PACF 图?
时间序列数据分析可应用于金融、经济和营销等多个领域。自相关函数 (ACF) 和偏自相关函数 (PACF) 广泛应用于时间序列数据分析。使用 PACF 图评估观测值之间的时间序列相关性。找到能够估计序列未来值的重要滞后值很有用。即便如此,如果您不熟悉 PACF 图,阅读起来可能很有挑战性。在这篇博客文章中,我们将帮助您完成理解时间序列分析的 PACF 图的每个步骤。
什么是 PACF?
偏自相关函数称为 PACF。在控制中间滞后的影响的情况下,它是一种用于时间序列分析的统计技术,用于评估给定滞后处的观察值与其先前延迟之间的直接联系。
换句话说,PACF 减去两个时间序列之间进一步延迟的影响,以评估它们在一定滞后处的值之间的相关性。另一方面,自相关函数 (ACF) 检查两个时间序列在一定滞后处的值之间的相关性,而不考虑中间延迟。在时间序列分析中检查自回归 (AR) 模型时,PACF 是一个有用的工具。可以使用 PACF 决定应包含在 AR 模型中的延迟顺序和数量。
PACF 图
时间序列的各种滞后设置的偏自相关值显示在 PACF 图上。PACF 图有助于识别重要的滞后值,以预测序列的未来值。换句话说,PACF 图中显著延迟的大小决定了时间序列的 AR(自回归)模型的位置。
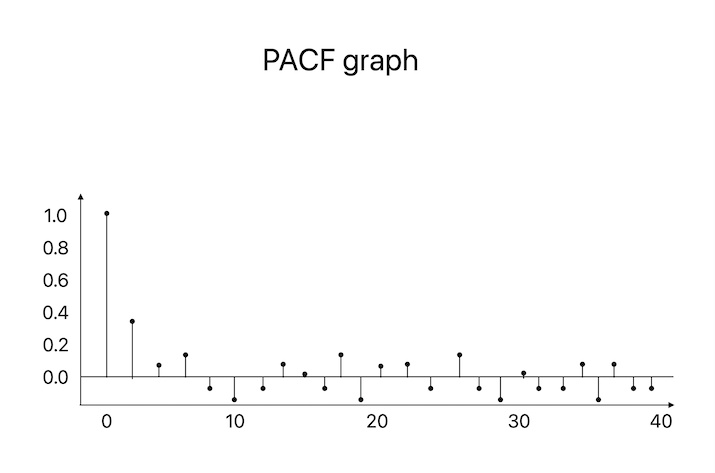
现在我们已经介绍了 PACF 和 PACF 图的基础知识,让我们看看如何解释 PACF 图。
步骤 1:确定滞后值的范围
确定滞后值的范围是理解 PACF 图的第一步。时间序列中两个观测值之间的时间距离称为滞后值。例如,如果您正在研究月度销售数据,滞后数将为一个月。
查看 PACF 图的 x 轴以找到滞后值的范围。偏自相关值表示在 y 轴上,而滞后值表示在 x 轴上。滞后值的典型范围(其中 n 是时间序列的长度)为 0 到 n-1。
步骤 2:确定显著性水平
下一步是确定相关性水平。当偏自相关值达到显著性水平时,它们被视为显著。在 PACF 图中,通常使用水平线来表示它。
样本大小和置信度都会影响显著性阈值。当使用 95% 置信度(标准)时,任何大于 95% 显著性阈值的偏自相关值都被视为显著。
步骤 3:解释 PACF 图
一旦确定了显著性水平和滞后值范围,就可以理解 PACF 图。理解 PACF 图的步骤如下 -
步骤 3.1:识别显著滞后
找到显著延迟是第一步。留意显著的偏自相关值。这些延迟值得注意,并显示了不同滞后结果之间的直接相关性。
步骤 3.2:确定 AR 模型的阶数
时间序列的 AR(自回归)模型的阶数部分由 PACF 图中的实际延迟决定。显著滞后值的数量决定了 AR 模型的阶数。例如,如果滞后值 1 和 2 很大,则 AR 模型的阶数将为 2。
步骤 3.3:检查截止点
截止点是评估 PACF 图时要考虑的关键因素。在较大的延迟之后,偏自相关值会逐渐下降,称为截止点。截止点意味着与不同滞后值直接相关的唯一滞后是重要延迟。如果没有截止,AR 模型还需要考虑与不同延迟值有直接联系的额外滞后。
步骤 3.4:解释非显著滞后
另一方面,PACF 图上的非显著滞后意味着该滞后值之间没有直接相关性。使用 AR 模型,可以忽略这些延迟。
偶尔可能会存在负且相当大的偏自相关值。这表明不同延迟的结果之间存在不良相关性。在这种情况下选择 AR 模型的阶数时,应考虑负相关性。
结论
总之,PACF 图是有效的时间序列分析工具,尤其是在查看 AR 模型时。它们有助于定位与不同延迟值密切相关的主要滞后值。查找滞后值的范围、显著性水平、显著滞后、AR 模型的阶数、截止值和非显著延迟都是解释 PACF 图所必需的。
如果您是时间序列分析的新手,阅读 PACF 图可能会有点令人生畏。然而,随着时间和精力的投入,您可以掌握阅读 PACF 图并将其应用于时间序列数据分析。


