如何在 MATLAB 中计算脉冲响应?
在本文中,我们将学习如何在 MATLAB 中计算系统的脉冲响应。脉冲响应是用于分析和理解系统对脉冲输入的行为的基本概念。
它主要用于分析线性时不变系统,如数字滤波器、电子电路、信号处理系统、控制系统等。
系统的脉冲响应可以定义如下:
当脉冲输入信号施加到系统时,系统的响应称为脉冲响应。对于连续时间系统,它表示为 h(t),对于离散时间系统,它表示为 h[n]。
脉冲响应用于指定系统在时间域中对脉冲输入信号的响应。其中,脉冲信号是幅度无限大且时间上无限小的信号。
从数学上讲,脉冲信号表示如下:
对于连续时间系统 (CTS)
$$\mathrm{\delta(t)\:=\:0;\:for\:t
eq 0}$$
$$\mathrm{\int_{−\infty}^{\infty}\delta(t)dt\:=\:1}$$
对于离散时间系统 (DTS)
$$\mathrm{\delta[n]\:=\:0;\:for\:n
eq 0}$$
$$\mathrm{\sum_{−\infty}^{\infty} \delta[n]\:=\:1}$$
总体而言,系统的脉冲响应使我们能够分析和研究系统行为的稳定性、时域特性、频率响应等。
在 MATLAB 中计算脉冲响应的算法
在 MATLAB 中计算系统脉冲响应的分步过程如下所述:
步骤 (1) - 通过系统的传递函数或其差分方程定义系统。
步骤 (2) - 使用 MATLAB 的内置函数"impulse"计算系统的脉冲响应。
步骤 (3) - 使用"plot"函数绘制系统的脉冲响应。此步骤以图形方式可视化脉冲响应。
现在,让我们考虑 MATLAB 中的几个示例程序来计算和可视化系统的脉冲响应。
示例 (1) - 一阶系统的脉冲响应
以下 MATLAB 程序演示了计算和可视化一阶系统的脉冲响应。
假设以下是表示一阶系统的传递函数:
$$\mathrm{H(s)\:=\:\frac{2}{3s+2}}$$
示例
% 用于计算二阶数字滤波器脉冲响应的 MATLAB 代码
% 指定滤波器的差分方程系数
ff = [0.7, 0.35, 0.55]; % 前馈系数
fb = 1; % 反馈系数,即无反馈
% 创建样本向量
n = 0:5; % 根据需要进行调整
% 计算系统的脉冲响应
h = impz(ff, fb, n);
% 绘制脉冲响应
stem(n, h); title('二阶数字滤波器的脉冲响应');
xlabel('样本索引 (n)');
ylabel('脉冲响应');
grid on;
输出
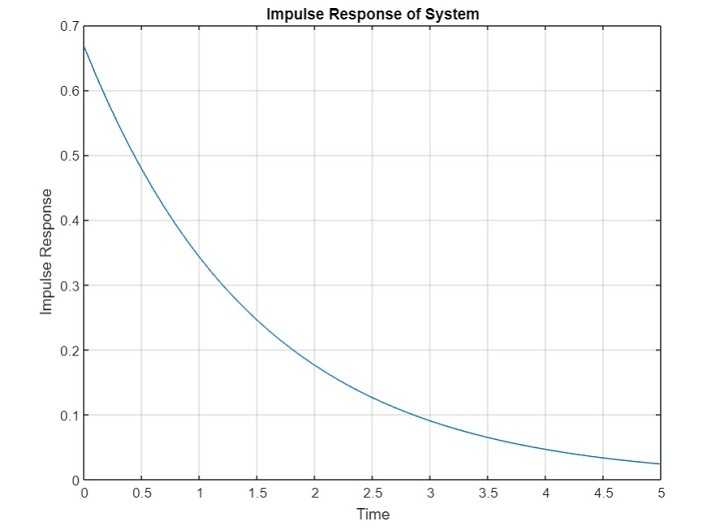
代码说明
在此 MATLAB 程序中,我们首先定义一阶系统的传递函数。然后,我们创建系统的传递函数模型。接下来,我们使用"impulse"函数计算系统的脉冲响应。最后,我们使用"plot"函数绘制系统的脉冲响应。
示例 (2) - 二阶递归数字滤波器的脉冲响应
以下 MATLAB 程序演示了具有无限脉冲响应的二阶递归数字滤波器的脉冲响应的计算。
让以下差分方程表示数字滤波器:
r[n] = 0.7c[n]+0.35c[n−1]+0.55c[n−2]
示例
% 用于计算二阶数字滤波器脉冲响应的 MATLAB 代码
% 指定滤波器的差分方程系数
ff = [0.7, 0.35, 0.55]; % 前馈系数
fb = 1; % 反馈系数,即无反馈
% 创建样本向量
n = 0:5; % 根据需要进行调整
% 计算系统的脉冲响应
h = impz(ff, fb, n);
% 绘制脉冲响应
stem(n, h); title('二阶数字滤波器的脉冲响应');
xlabel('样本索引 (n)');
ylabel('脉冲响应');
grid on;
输出

代码说明
在此 MATLAB 程序中,我们首先定义一阶系统的传递函数。然后,我们创建系统的传递函数模型。接下来,我们使用"impulse"函数计算系统的脉冲响应。最后,我们使用"plot"函数绘制系统的脉冲响应。
结论
因此,这就是使用 MATLAB 计算系统脉冲响应的全部内容。MATLAB 提供了两个内置函数,即"impulse"和"impz",分别用于计算连续时间系统和离散时间系统的脉冲响应。上面的示例程序说明了如何使用这些函数来计算脉冲响应。


