使用 Python 中的 NumPy 生成具有给定根的 Hermite_e 级数
Hermite 多项式是一组正交多项式,可用于各种数学应用。它们通常用于微分方程、概率论和量子力学的解。Hermite_e 级数是 Hermite 多项式的变体,用于用根来表示函数。在本文中,我们将讨论如何使用 Python 中的 NumPy 生成具有给定根的 Hermite_e 级数。
安装和语法
NumPy 是一个提供数值运算支持的 Python 库,可以使用 pip 安装并使用语句"import numpy"导入 Python。
pip install numpy
要使用 NumPy 生成具有给定根的 Hermite_e 级数,可以使用以下语法 -
numpy.polynomial.hermite_e.hermegauss(roots, deg)
roots - 包含 Hermite_e 级数根的一维数组。
deg − Hermite_e 级数的度数。
算法
以下是使用 NumPy 生成具有给定根的 Hermite_e 级数的算法 −
导入 NumPy 库。
定义一个包含 Hermite_e 级数根的数组。
定义 Hermite_e 级数的度数。
使用根和度数作为参数调用 numpy.polynomial.hermite_e.hermegauss() 函数。
该函数返回两个数组,一个包含权重,另一个包含 Hermite_e 级数的节点。
使用权重和节点构造 Hermite_e系列。
示例 1
以下代码示例生成一个 Hermite_e 系列,其根为 [-1, 0, 1],度为 2。
import numpy as np roots = np.array([-1, 0, 1]) deg = 2 weights, nodes = np.polynomial.hermite_e.hermegauss(deg) print(weights) print(nodes)
输出
[-1. 1.] [1.25331414 1.25331414]
示例 2
以下代码示例生成一个 Hermite_e 级数,其根为 [1, 2, 3, 4],度为 3。
import numpy as np
# 根数组
roots = np.array([0, 1, 2, 3])
# 用零初始化系数数组
coeffs = np.zeros((len(roots), 2 * len(roots) - 1))
# 设置系数的初始值
coeffs[:, 0] = roots # 将 f(x) 值设置为根
coeffs[1:, 1] = np.diff(coeffs[:, 0]) / np.diff(roots) # 使用有限差分方法设置 f'(x) 值
# 设置使用递归关系计算剩余系数
for j in range(2, 2 * len(roots)):
for i in range(len(roots)):
if j % 2 == 0 and i >= j // 2:
# 偶数指数系数
coeffs[i, j // 2] = coeffs[i, j // 2 - 1] * (j - 1) / (j // 2)
elif j % 2 == 1 and i >= (j + 1) // 2:
# 奇数索引系数
coeffs[i, (j + 1) // 2 - 1] = (coeffs[i, j // 2] - coeffs[i - 1, j // 2]) / (roots[i] - roots[i - j // 2])
# 使用计算出的系数生成 Hermite 级数
def hermite_e_series(x):
res = np.zeros_like(x)
for i in range(len(roots)):
term = np.ones_like(x)
for j in range(i):
term *= (x - roots[j])
res += coeffs[i, i] * term
return res
x = np.linspace(-1, 4, 1000)
y = hermite_e_series(x)
# 获取前 10 个系数
print(y[:10])
# 绘制函数
import matplotlib.pyplot as plt
plt.plot(x, y)
plt.show()
输出
[-5.5 -5.44884884 -5.39799735 -5.34744457 -5.29718957 -5.24723141 -5.19756916 -5.14820186 -5.09912858 -5.05034838]
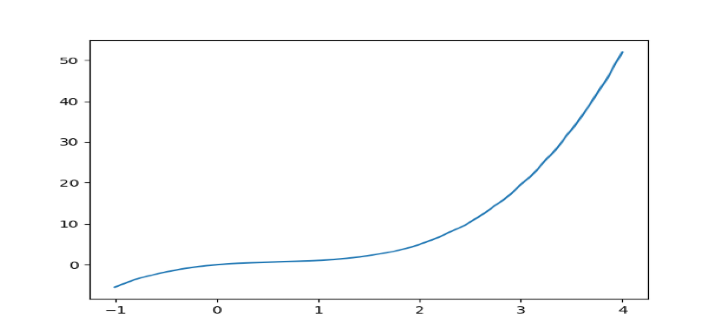
以下代码示例生成一个根为 [0, 1, 2, 3]、度为 4 的 Hermite_e 级数,并使用 Matplotlib 绘制该级数。
应用
使用 Python 中的 NumPy 生成的 Hermite 级数有多种应用。在物理学中,Hermite 多项式用于描述量子谐振子的波函数,同时也证明它对于数值分析和科学计算以及实现统计学中的近似函数(例如正态分布)非常有用,因为它经常用高精度的近似函数来实现。
结论
Hermite_e 级数是科学计算和数值分析中的强大工具。借助 Python 中的 NumPy,生成 Hermite 级数已成为一项简单的任务。生成级数的算法包括设置初始系数,然后使用递归关系确定剩余系数。一旦计算出系数,就可以使用简单的函数生成 Hermite 级数。该级数在物理学、数学和统计学中有着广泛的应用。通过使用 Hermite_e 级数,科学家和数学家可以高精度地近似复杂函数,使其成为许多研究领域的宝贵工具。


