C++ 中的二叉树层次遍历
c++server side programmingprogramming更新于 2024/9/1 20:45:00
假设我们有一棵二叉树。我们必须使用层次遍历方案来遍历这棵树。因此,如果树是这样的
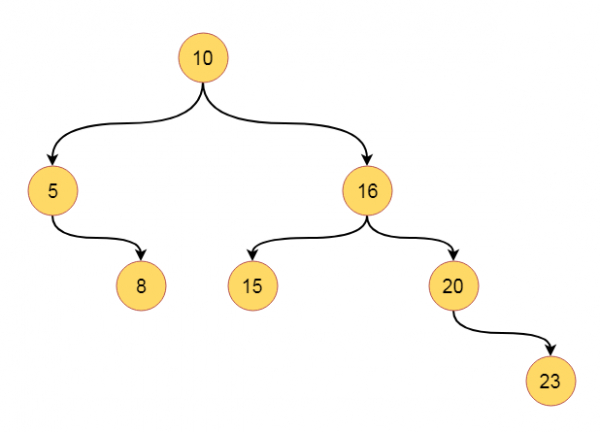
遍历顺序将类似于 − [10, 5, 16, 8, 15, 20, 23]
为了解决这个问题,我们将遵循以下步骤 −
- 定义队列 que 来存储节点
- 将根插入队列。
- 当 que 不为空时,执行
- item := item 存在于队列的最前面
- 打印 item 的值
- 如果 item 的左侧不为空,则将 item 的左侧插入队列
- 如果 item 的右侧不为空,则将 item 的右侧插入队列
- 从 que 中删除最前面的元素
示例(C++)
让我们看下面的实现,以便更好地理解 −
#include<iostream>
#include<queue>
使用命名空间 std;
类节点{
public:
int h_left, h_right, bf, value;
节点 *left, *right;
};
类树{
private:
节点 *get_node(int key);
public:
节点 *root;
tree(){
root = NULL; //在开始时将 root 设置为 NULL
}
void levelorder_traversal(node *r);
node *insert_node(node *root, int key);
};
node *tree::get_node(int key){
node *new_node;
new_node = new node; //动态创建一个新节点
new_node->h_left = 0; new_node->h_right = 0;
new_node->bf = 0;
new_node->value = key; //存储给定键的值
new_node->left = NULL; new_node->right = NULL;
return new_node;
}
void tree::levelorder_traversal(node *root){
queue <node*> que;
node *item;
que.push(root); //首先插入根节点
while(!que.empty()){
item = que.front(); //从最前端获取元素
cout << item->value << &" &";;
if(item->left != NULL) //当左子节点存在时,插入队列
que.push(item->left);
if(item->right != NULL) //当右子节点存在时,插入队列
que.push(item->right);
que.pop(); //从队列中删除项目
}
}
node *tree::insert_node(node *root, int key){
if(root == NULL){
return (get_node(key)); //当树为空时,创建一个节点作为根节点
}
if(key < root->value){ //当key小于根节点值时,向左移动
root->left = insert_node(root->left, key);
}
else if(key > root->value){ //当key大于根节点值时,向右移动
root->right = insert_node(root->right, key);
}
return root; //当key已经存在时,不要再次插入
}
main(){
node *root;
tree my_tree;
//将一些键插入树中。
my_tree.root = my_tree.insert_node(my_tree.root, 10);
my_tree.root = my_tree.insert_node(my_tree.root, 5);
my_tree.root = my_tree.insert_node(my_tree.root, 16);
my_tree.root = my_tree.insert_node(my_tree.root, 20);
my_tree.root = my_tree.insert_node(my_tree.root, 15);
my_tree.root = my_tree.insert_node(my_tree.root, 8);
my_tree.root = my_tree.insert_node(my_tree.root, 23);
cout << "Level-Order Traversal: ";
my_tree.levelorder_traversal(my_tree.root);
}
输入
[10,5,16,null,8,15,20,null,null,null,null,null,null,null,23]
输出
Level-Order Traversal: 10 5 16 8 15 20 23

