使用 Python 将 K 乘以每个第 N 个元素
在此问题陈述中,我们需要将 K 乘以给定列表或序列中的每个第 N 个项目,并使用 Python 实现解决方案。因此,我们将使用基本的 Python 编程来解决这个问题。
理解问题
当前的问题是,我们必须将一个称为 K 的特定值乘以给定列表中的每个第 N 个项目。通常,我们会创建一个函数来应用于列表的每个项目,但在我们的问题中,我们必须将一个常数与列表中的某些项目相乘。为了更好地理解,让我们深入研究以下示例:
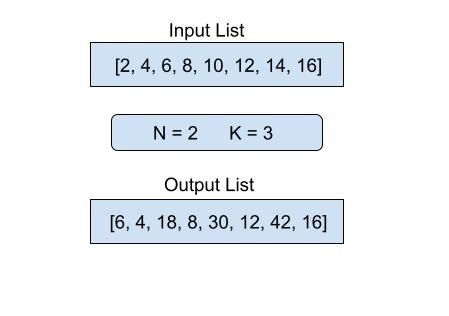
上述问题的逻辑
为了解决给定问题,即在每个第 N 个项目中乘以 K,我们将使用 for 循环遍历列表并查找位于 N 倍数位置的项目。之后,我们将每个第 N 个项目乘以 K 的值。这个过程将继续,直到所有第 N 个项目都不会乘以 K。
算法
步骤 1 - 通过定义名为 multiply_nth_item 的函数来启动算法,以将 K 与给定序列中的每个第 N 个项目相乘。此函数将接受三个参数,如系列、K 和 N。这里的系列是项目的序列,K 是我们必须在第 N 个项目中相乘的值。
步骤 2 - 初始化一个变量来跟踪计数,并将其命名为 count,其初始值为 1。
步骤 3 - 接下来使用 for 循环遍历给定输入系列中的每个项目。
步骤 4 - 现在我们将检查条件,如果 count 的值可以被 N 整除,那么我们将该项目与 K 的值相乘。
步骤 5 - 如果上述条件为假,那么我们将 count 的值增加 1。
步骤 6 - 最后我们将返回修改后的系列。
示例
# 定义将 k 乘以第 n 项的函数
def multiply_nth_item(series, K, N):
count = 1
for i in range(len(series)):
if count % N == 0:
series[i] *= K
count += 1
return series
# 初始化系列,K 和 N
input_series = [11, 12, 13, 14, 15, 16, 17, 18, 19, 20]
K = 3
N = 2
#调用函数
Output = multiply_nth_item(input_series, K, N)
print(Output)
输出
[11, 36, 13, 42, 15, 48, 17, 54, 19, 60]
算法 - 使用 Numpy
步骤 1 − 由于我们使用 numpy 来解决此算法中的给定问题,因此导入 numpy库。
步骤 2 - 将函数定义为 multiply_nth_item 并传递三个参数,分别为 series、K 和 N。series 是输入列表,K 是要相乘的值,N 是要更新的项目的位置。
步骤 3 - 根据给定的输入系列创建一个 numpy 数组,因为我们需要每个项目的索引。
步骤 4 - 该数组将显示给定系列中每个项目的位置。
步骤 5 - 之后,我们将借助它创建一个位置变量,并检查索引是否可以被 N 整除。如果条件为真,我们将通过与 K 相乘来更新它。
步骤 6 - 位置变量将用于更新系列中的选定项目。
步骤 7 - 现在再次借助 tolist 函数将 numpy 数组转换为常规 Python 列表。
示例 - 使用 Numpy
# 导入 numpy 库 import numpy as np # 定义函数以乘以 K def multiply_nth_item(series, K, N): series = np.array(series) index = np.arange(len(series)) position = index % N == 0 series[position] *= K return series.tolist() # 初始化系列、K 和 N input_series = [2, 4, 6, 8, 10, 12, 14, 16, 18, 20] K = 3 N = 2 # 调用函数 Output = multiply_nth_item(input_series, K, N) print(Output)
输出
[6, 4, 18, 8, 30, 12, 42, 16, 54, 20]
复杂度
如果给定列表中存在 n 个项目,则使用 Python 将 K 与每个第 N 个项目相乘的时间复杂度为 O(n)。因为我们在两种方法中都使用了基本的迭代过程来乘以序列中的每第 N 个项。
结论
因此,使用 Python 将 K 与给定序列中的每第 N 个项相乘可以通过上述算法实现,时间复杂度为 O(n)。并且两种算法的时间复杂度都是线性的,这表明算法是有效的。


