如何在 Python 中执行卡方拟合优度检验
简介
数据科学家经常使用统计方法进行假设检验,以从数据集中获得见解。虽然有多种统计方法可用,但本文将讨论卡方拟合优度检验及其在 Python 中的实现。卡方检验将观察到的分类变量分布验证为预期分布。它告诉我们可用的事件值是否与预期值不同。
卡方检验
您可以执行卡方检验来验证观察到的事件的数据集分布。卡方检验做出了一些假设,如下所示 -
变量是独立的。
仅存在一个分类特征。
每个变量必须包含具有五个以上频率计数的类别。
随机抽样的数据集。
每个数据组必须在频率计数中显示相互排斥性。
卡方检验统计量
卡方检验使用以下公式给出统计输出 -
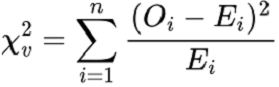
其中
v 表示自由度
O 表示样本观测值
E 代表总体预期值
n 表示变量类别计数。
现在让我们学习如何执行卡方检验。
假设检验步骤
执行卡方检验有几个步骤,如下所示 -
首先,您需要创建一个零假设 H0 和一个替代假设假设,H1。
然后,您需要确定接受或拒绝零假设的概率阈值。此阈值的典型值为 5%,相应的临界值取决于分布。
然后使用上述公式计算卡方统计量。
最后,您需要将检验统计值与临界值进行比较。如果检验统计量大于临界值,则我们拒绝零假设;否则,我们无法拒绝零假设。
让我们使用上述步骤实施测试 −
这里,零假设是变量以预定的方式分布。而备择假设是变量没有不同的分布。我们将使用两种方法实现卡方检验,如下所述 -
使用内置函数实现卡方
语法
chi_square_test_statistic, p_value = stats.chisquare( experience_in_years, Salary)
此函数采用两个特征,对它们应用卡方公式,并返回卡方检验统计量和 p_value。
算法
加载所需的依赖项,如 scipy 和 numpy。
将特征传递给要对其应用检验统计量的 scipy.stats 的卡方函数。
获取检验统计量和 p_value。
根据 p 值和卡方统计量接受或拒绝零假设和备择假设。
示例
该过程从加载所有必要的依赖项开始。
# 导入包 import scipy.stats as stats import numpy as np
让我们准备一个演示数据,其中有两列"experience_in_years"和"salary"。对于这些数据,我们将执行卡方检验。
# 员工的工作年限
# 每年的薪资待遇(十万卢比)
experience_in_years= [8, 6, 10, 7, 8, 11, 9]
Salary= [9, 8, 11, 8, 10, 7, 6]
# 卡方拟合优度检验
chi_square_test_statistic, p_value = stats.chisquare(
experience_in_years, Salary)
# 卡方检验统计量和 p 值
print('chi_square_test_statistic is : ' +
str(chi_square_test_statistic))
print('p_value : ' + str(p_value))
# 查找卡方临界值
print(stats.chi2.ppf(1-0.05, df=6))
解释
上述代码是使用 Scipy 库中的内置函数对卡方检验的 Python 实现。chisquare 方法从 stats 导入,它返回两个值:chi_square_test_statistic 和 p-value。此方法采用两个特征,将比较两个变量并应用上述卡方公式来计算卡方统计数据。在这里,我们比较的是工作年限和年薪之间的关系。
输出
chi_square_test_statistic 为:5.0127344877344875 p_value :0.542180861413329 12.591587243743977
我们在这里可以看到,p 值为 0.54,临界值为 12.59。检验统计量小于临界值,因此我们可以接受零假设并拒绝备择假设。
从 Scratch 实现卡方
算法
chi_square_test_statistic1 = chi_square_test_statistic1 + \ (np.square(experience_in_years[i]-salary[i]))/salary[i]
使用上述公式计算数据集中每个样本的卡方值,并将它们相加得到最终分数。
算法
加载所需的依赖项,如 numpy。
初始化一个值为 0 的变量,该变量将存储最终值统计量。
对数据中的每个样本进行迭代,计算每个样本的统计量,并将其添加到包含统计量最终值的变量中。
计算出统计量后,接受或拒绝原假设和备择假设。
示例
此方法将使用公式实现卡方拟合优度检验。此方法将产生与上述方法相同的结果。
import scipy.stats as stats
import numpy as np
# 员工的工作年限
# 以十万卢比为单位的年薪待遇
experience_in_years= [8, 6, 10, 7, 8, 11, 9]
salary= [9, 8, 11, 8, 10, 7, 6]
# 使用公式确定卡方拟合优度
chi_square_test_statistic1 = 0
for i in range(len(experience_in_years)):
chi_square_test_statistic1 = chi_square_test_statistic1 + \
(np.square(experience_in_years[i]-salary[i]))/salary[i]
print('由公式确定的卡方值:' +
str(chi_square_test_statistic1))
# 查找卡方临界值
print(stats.chi2.ppf(1-0.05, df=6))
解释
上述代码已在 Python 中实现,用于对相同数据执行卡方检验。在此方法中,我们仅在 Python 中实现了卡方统计公式,而不是导入内置方法。for 循环有助于遍历数据集。然后,我们用 NumPy 实现上述公式,并将分数与之前的分数相加,以获得整个数据集的总体分数。最后,我们检查使用此方法获得的卡方统计数据。
输出
由公式确定的卡方值:5.0127344877344875 12.591587243743977
正如我们预期的那样,结果与使用以前的方法得到的结果相同。这个结果还表明我们不应该拒绝原假设,但我们可以拒绝备择假设。
结论
我们已经了解了卡方拟合优度检验以及如何使用 Python 实现它。让我们用几个关键点来总结一下这篇文章 -
卡方检验验证了观察到的分类变量的分布与预期变量分布的一致性。
卡方检验做出了一些假设,包括只有一个分类变量、独立变量、至少五个唯一类别和随机抽样数据。
我们通过接受或拒绝零假设来得出检验结果。
阈值必须小于接受零假设的临界值。


