使用 Floyd Warshall 算法查找任意两个节点之间的最短路径
C++ 有一个宏,它被定义为一段代码或所需值,并且它会在用户需要时反复使用。Floyd Warshall 算法是在给定加权图中查找所有顶点对之间的最短路径的过程。该算法遵循动态规划方法来找到最小权重图。
让我们借助图表了解什么是 Floyd Warshall 算法 −
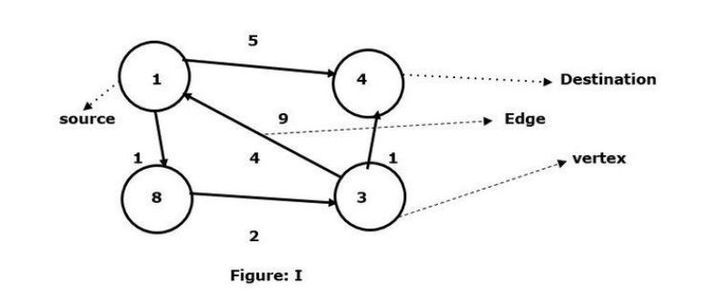
以顶点 1 为源,以顶点 4 为目的地,找到它们之间的最短路径。
我们已经看到有两条路径可以连接到目的地顶点 4。
1 -> 4 – 边权重为 5
1 -> 8 -> 3 -> 4 – 边权重 ( 1+2+1 ) 为 4。
在给定的图 I 中,我们看到两个顶点之间连接的最小边。因此,这里顶点 8 和顶点 3 连接顶点 1 到顶点 4 的路径,边的最小权重为 4。另一方面,顶点 1 到顶点 4 之间有一条有向边,边的权重为 5。
现在我们比较两个权重,即 4 和 5。因此,这里 4 是 Floyd Warshall 算法中图的最小权重。
在本文中,我们将使用 Floyd Warshall 算法解决任意两个给定节点之间的最短路径。
语法
程序中使用以下语法 -
data_type[][] array_name;
参数
data_type[][] - 用户提到的数据类型。第一个数组表示行,而第二个数组表示列。因此,这代表二维数组。
array_name - 给数组的名称。
算法
我们将使用头文件'iostream'启动程序,并将宏位置定义为'INF'(无穷大),因为稍后它将满足 2D 数组矩阵和 if-else 语句。
接下来,我们创建名为'printPath'的全局函数定义,并接受三个参数,即'parent[]'、'i'和'j',以验证路径是否存在。
然后我们启动主函数并将值'4'存储到表示顶点数量的变量'V'中。其次,将邻接矩阵形式的值存储到'dist[V][V]'变量中。我们知道 dist[i][j] 表示二维矩阵,它通过存储邻接矩阵来定义从 'i' 到 'j' 的边的权重。
接下来,我们初始化 'parent' 变量的二维数组,其大小为 [V][V]。
在这个变量中,我们用来显示相对于 'parent[i][j]' 的每对顶点 'i' 和 'j'。
通过使用两个嵌套的 for 循环,我们将找到最短路径。第一个 for 循环迭代矩阵中的行。继续进行第二个 for 循环,它会迭代矩阵中的列,然后我们将使用 if-else 语句检查以下条件 -
if (dist[i][j] != INF && i != j){ parent[i][j] = i;>
在 if 语句中,我们使用 'and' (&&) 运算符来显示两个条件,如果这两个条件都满足,则'i'将存储到'parent[i][j]',这验证了路径是否存在。
else { parent[i][j] = -1;>
在 else 语句中,我们将'-1'初始化为'parent[i][j]',这验证了路径不存在。
现在我们从三个嵌套开始for 循环并应用 0 到 V-1 范围内的 k 个顶点,借助此范围,我们的最短距离和路径将被更新。在第三个嵌套循环中,我们使用以下条件,例如
if (dist[i][j] < dist[i][k] + dist[k][j]){
dist[i][j] = dist[i][k] + dist[k][j];
parent[i][j] = parent[k][j];
}
接下来,我们通过给出以下条件来打印所有顶点对的最短距离和路径,例如
通过使用两个嵌套的 for 循环,我们打印最短距离和路径。
通过在第二个 for 循环下使用 if 语句,我们将检查 dist[i][j] 是否等于无穷大。如果发现无穷大,则将打印"INF",否则将打印最短路径。
最后,我们调用名为"printPath()"的函数,通过传递三个参数(即parent[i]、i和j)来获取最短路径的值。
这里 K 正在更新二维数组矩阵中的行和列部分,这将验证新更新的最短路径和距离。
示例
在此程序中,我们将使用Floyd Warshall算法计算任意两个节点之间的最短路径。
#include <iostream>
using namespace std;
#define INF 1000000000 // Infinity
void printPath(int parent[], int i, int j) {
if (i == j)
cout << i << " ";
else if (parent[j] == -1)
cout << "No path exists";
else
{
printPath(parent, i, parent[j]);
cout << j << " ";
}
}
int main()
{
int V = 4;
// V 表示顶点数
int dist[V][V] = {{0, 2, INF, 4},
{6, 0, 5, 3},
{INF, 10, 0, 1},
{7, 9, 8, 0}};
// 使用邻接矩阵表示图
// 应用 Floyd Warshall 算法查找最短路径
int parent[V][V];
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V; j++)
{
if (dist[i][j] != INF && i != j)
parent[i][j] = i;
else
parent[i][j] = -1;
}
}
// 使用从 0 到 V-1 的 k 个顶点范围更新路径和距离。
for (int k = 0; k < V; k++)
{
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V; j++)
{
if (dist[i][j] > dist[i][k] + dist[k][j])
{
dist[i][j] = dist[i][k] + dist[k][j];
parent[i][j] = parent[k][j];
}
}
}
}
// 打印所有顶点对之间的最短距离和路径
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V; j++)
{
cout << "" << i << " 和 " << j << " 之间的最短距离为 ";
if (dist[i][j] == INF)
cout << "INF ";
else
cout << dist[i][j] << " ";
cout << " 最短路径为:- ";
printPath(parent[i], i, j);
cout << endl;
}
}
return 0;
}
输出
0 和 0 之间的最短距离为 0,最短路径为:- 0 0 和 1 之间的最短距离为 2,最短路径为:- 0 1 0 和 2 之间的最短距离为 7,最短路径为:- 0 1 2 0 和 3 之间的最短距离为 4,最短路径为:- 0 3 1 和 0 之间的最短距离为 6,最短路径为:- 1 0 1 和 1 之间的最短距离为 0,最短路径为:- 1 1 和 2 之间的最短距离为 5,最短路径为:- 1 2 1 和 3 之间的最短距离为 3,最短路径为:- 1 3 最短距离2 和 0 之间的最短距离是 8,最短路径是:- 2 3 0 2 和 1 之间的最短距离是 10,最短路径是:- 2 1 2 和 2 之间的最短距离是 0,最短路径是:- 2 2 和 3 之间的最短距离是 1,最短路径是:- 2 3 3 和 0 之间的最短距离是 7,最短路径是:- 3 0 3 和 1 之间的最短距离是 9,最短路径是:- 3 1 3 和 2 之间的最短距离是 8,最短路径是:- 3 2 3 和 3 之间的最短距离是 0,最短路径是:- 3
结论
我们使用 Floyd Warshall 算法学习了任意两个节点之间最短路径的概念。我们使用邻接矩阵作为程序的输入,在其中找到最短路径和距离。除了更新路径和距离之外,我们还使用 k 个顶点来更新行和列。在我们的日常生活中,我们在 Google 地图上搜索从一个源到目的地的最短路线或路径。


