Javascript 中的深度优先搜索遍历
javascriptweb developmentfront end technology
DFS 在访问兄弟顶点之前先访问子顶点;也就是说,它在探索任何特定路径的广度之前先遍历其深度。实现算法时通常使用堆栈(通常是程序通过递归调用的堆栈)。
以下是 DFS 的工作原理 −
- 访问相邻的未访问顶点。将其标记为已访问。显示它。将其推入堆栈。
- 如果未找到相邻顶点,则从堆栈中弹出一个顶点。 (它将弹出堆栈中所有没有相邻顶点的顶点。)
- 重复规则 1 和规则 2,直到堆栈为空。
让我们看一下 DFS 遍历的工作原理。
| 步骤 | 遍历 | 描述 |
|---|---|---|
| 1 | 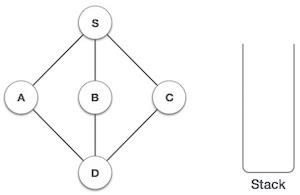 | 初始化堆栈。 |
| 2 | 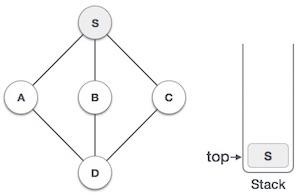 | 将 S 标记为已访问并将其放入堆栈。从 S 探索任何未访问的相邻节点。我们有三个节点,我们可以选择其中任何一个。在此示例中,我们将按字母顺序获取节点。 |
| 3 | 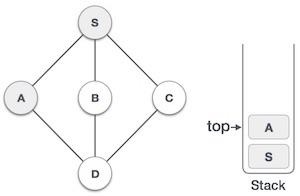 | 将 A 标记为已访问并将其放入堆栈。从 A 探索任何未访问的相邻节点。 S 和 D 都与 A 相邻,但我们只关注未访问的节点。 |
| 4 | 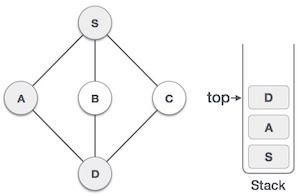 | 访问 D 并将其标记为已访问并放入堆栈。这里,我们有 B 和 C 节点,它们与 D 相邻,并且都未被访问过。但是,我们还是要按照字母顺序进行选择。 |
| 5 | 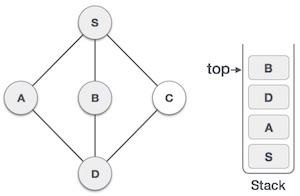 | 我们选择 B,将其标记为已访问并放入堆栈。这里 B 没有任何未访问的相邻节点。因此,我们从堆栈中弹出 B。 |
| 6 | 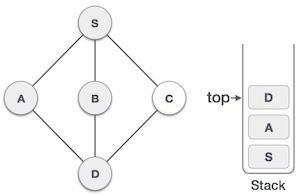 | 我们检查堆栈顶部是否返回到前一个节点,并检查它是否有任何未访问的节点。在这里,我们发现 D 位于堆栈顶部。 |
| 7 | 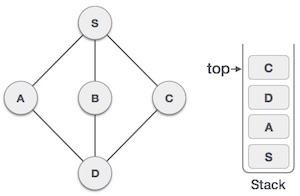 | 现在只有来自 D 的未访问相邻节点是 C。所以我们访问 C,将其标记为已访问并将其放入堆栈。 |
由于 C 没有任何未访问的相邻节点,因此我们不断弹出堆栈,直到找到具有未访问相邻节点的节点。在这种情况下,没有未访问的相邻节点,我们继续弹出直到堆栈为空。让我们看看如何在 JavaScript 中实现这一点。
示例
DFS(node) {
// 创建一个 Stack 并在其中添加我们的初始节点
let s = new Stack(this.nodes.length);
let explored = new Set();
s.push(node);
// 将第一个节点标记为已探索
explored.add(node);
// 我们将继续,直到 Stack 变空
while (!s.isEmpty()) {
let t = s.pop();
// 记录从 Stack 中出来的每个元素
console.log(t);
// 1. 在边对象中,我们搜索此节点直接连接到的节点。
// 2. 我们过滤掉已经被探索过的节点。
// 3. 然后我们将每个未探索的节点标记为已探索并将其推送到堆栈。
this.edges[t]
.filter(n => !explored.has(n))
.forEach(n => {
explored.add(n);
s.push(n);
});
}
}
嗯,这很简单。我们实际上只是将队列换成了堆栈,然后我们就有了 DFS。这实际上是两者之间的唯一区别。DFS 也可以使用递归来实现。但在这种情况下最好避免这种情况,因为更大的图意味着我们需要额外的内存来跟踪调用堆栈。
您可以使用以下方法进行测试 −
let g = new Graph();
g.addNode("A");
g.addNode("B");
g.addNode("C");
g.addNode("D");
g.addNode("E");
g.addNode("F");
g.addNode("G");
g.addEdge("A", "C");
g.addEdge("A", "B");
g.addEdge("A", "D");
g.addEdge("D", "E");
g.addEdge("E", "F");
g.addEdge("B", "G");
g.DFS("A");
输出
This will give the output.
A D E F B G C


