C++ 程序实现 AVL 树
c++server side programmingprogramming
AVL 树是一种自平衡二叉搜索树,其中所有节点的左子树和右子树的高度差不能超过 1。
树旋转是一种改变结构而不干扰 AVL 树上元素顺序的操作。它在树中将一个节点向上移动,将一个节点向下移动。它用于改变树的形状,并通过将较小的子树向下移动和将较大的子树向上移动来降低其高度,从而提高许多树操作的性能。旋转的方向取决于树节点移动到哪一侧,而另一些人则认为它取决于哪个子节点占据了根的位置。这是一个实现 AVL 树的 C++ 程序。
函数说明:
height(avl *):计算给定 AVL 树的高度。
difference(avl *):计算给定树的子树高度之间的差异
avl *rr_rotat(avl *):右-右旋转是右旋转和右旋转的组合。
avl *ll_rotat(avl *):左-左旋转是左旋转和左旋转的组合。
avl *lr_rotat(avl*):左-右旋转是左旋转和右旋转的组合。
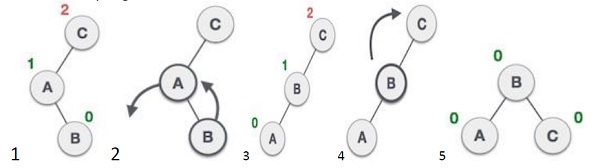
avl *rl_rotat(avl *):右旋转和左旋转的组合。
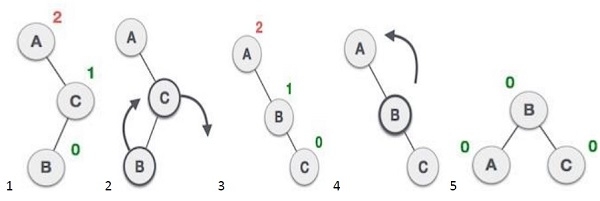
avl * balance(avl *):通过获取平衡因子对树执行平衡操作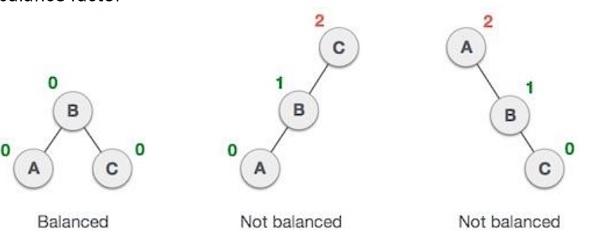
avl * insert(avl*, int):执行插入操作。使用此函数在树中插入值。
show(avl*, int):显示树的值。
inorder(avl *):按顺序遍历树。
preorder(avl *):以前序方式遍历树。
postorder(avl*):以后序方式遍历树
示例代码
#include<iostream>
#include<cstdio>
#include<sstream>
#include<algorithm>
#define pow2(n) (1 << (n))
using namespace std;
struct avl {
int d;
struct avl *l;
struct avl *r;
}*r;
class avl_tree {
public:
int height(avl *);
int difference(avl *);
avl *rr_rotat(avl *);
avl *ll_rotat(avl *);
avl *lr_rotat(avl*);
avl *rl_rotat(avl *);
avl * balance(avl *);
avl * insert(avl*, int);
void show(avl*, int);
void inorder(avl *);
void preorder(avl *);
void postorder(avl*);
avl_tree() {
r = NULL;
}
};
int avl_tree::height(avl *t) {
int h = 0;
if (t != NULL) {
int l_height = height(t->l);
int r_height = height(t->r);
int max_height = max(l_height, r_height);
h = max_height + 1;
}
return h;
}
int avl_tree::difference(avl *t) {
int l_height = height(t->l);
int r_height = height(t->r);
int b_factor = l_height - r_height;
return b_factor;
}
avl *avl_tree::rr_rotat(avl *parent) {
avl *t;
t = parent->r;
parent->r = t->l;
t->l = parent;
cout<<"Right-Right Rotation";
return t;
}
avl *avl_tree::ll_rotat(avl *parent) {
avl *t;
t = parent->l;
parent->l = t->r;
t->r = parent;
cout<<"Left-Left Rotation";
return t;
}
avl *avl_tree::lr_rotat(avl *parent) {
avl *t;
t = parent->l;
parent->l = rr_rotat(t);
cout<<"Left-Right Rotation";
return ll_rotat(parent);
}
avl *avl_tree::rl_rotat(avl *parent) {
avl *t;
t = parent->r;
parent->r = ll_rotat(t);
cout<<"Right-Left Rotation";
return rr_rotat(parent);
}
avl *avl_tree::balance(avl *t) {
int bal_factor = difference(t);
if (bal_factor > 1) {
if (difference(t->l) > 0)
t = ll_rotat(t);
else
t = lr_rotat(t);
} else if (bal_factor < -1) {
if (difference(t->r) > 0)
t = rl_rotat(t);
else
t = rr_rotat(t);
}
return t;
}
avl *avl_tree::insert(avl *r, int v) {
if (r == NULL) {
r = new avl;
r->d = v;
r->l = NULL;
r->r = NULL;
return r;
} else if (v< r->d) {
r->l = insert(r->l, v);
r = balance(r);
} else if (v >= r->d) {
r->r = insert(r->r, v);
r = balance(r);
} return r;
}
void avl_tree::show(avl *p, int l) {
int i;
if (p != NULL) {
show(p->r, l+ 1);
cout<<" ";
if (p == r)
cout << "Root -> ";
for (i = 0; i < l&& p != r; i++)
cout << " ";
cout << p->d;
show(p->l, l + 1);
}
}
void avl_tree::inorder(avl *t) {
if (t == NULL)
return;
inorder(t->l);
cout << t->d << " ";
inorder(t->r);
}
void avl_tree::preorder(avl *t) {
if (t == NULL)
return;
cout << t->d << " ";
preorder(t->l);
preorder(t->r);
}
void avl_tree::postorder(avl *t) {
if (t == NULL)
return;
postorder(t ->l);
postorder(t ->r);
cout << t->d << " ";
}
int main() {
int c, i;
avl_tree avl;
while (1) {
cout << "1.Insert Element into the tree" << endl;
cout << "2.show Balanced AVL Tree" << endl;
cout << "3.InOrder traversal" << endl;
cout << "4.PreOrder traversal" << endl;
cout << "5.PostOrder traversal" << endl;
cout << "6.Exit" << endl;
cout << "Enter your Choice: ";
cin >> c;
switch (c) {
case 1:
cout << "Enter value to be inserted: ";
cin >> i;
r = avl.insert(r, i);
break;
case 2:
if (r == NULL) {
cout << "Tree is Empty" << endl;
continue;
}
cout << "Balanced AVL Tree:" << endl;
avl.show(r, 1);
cout<<endl;
break;
case 3:
cout << "Inorder Traversal:" << endl;
avl.inorder(r);
cout << endl;
break;
case 4:
cout << "Preorder Traversal:" << endl;
avl.preorder(r);
cout << endl;
break;
case 5:
cout << "Postorder Traversal:" << endl;
avl.postorder(r);
cout << endl;
break;
case 6:
exit(1);
break;
default:
cout << "Wrong Choice" << endl;
}
}
return 0;
}
输出
1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 13 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 10 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 15 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 5 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 11 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 4 Left-Left Rotation1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 8 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 16 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 3 Inorder Traversal: 4 5 8 10 11 13 15 16 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 4 Preorder Traversal: 10 5 4 8 13 11 15 16 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 5 Postorder Traversal: 4 8 5 11 16 15 13 10 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 14 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 3 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 7 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 9 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 52 Right-Right Rotation 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 6


