具有最大弯曲数的 C++ 路径长度
c++server side programmingprogramming
为了解决给定二叉树的问题。现在我们需要找到具有最大弯曲数的路径。即,当路径的方向从左变为右或从右变为左时,即为弯曲,例如
输入 −
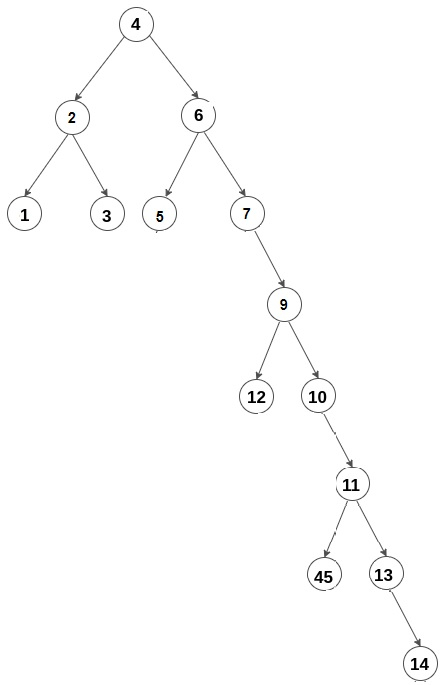
输出 −
6
现在,在这种方法中,我们将遍历树并跟踪先前的移动。如果方向发生变化,我们只需更新弯道数,然后找到最大值。
寻找解决方案的方法
在这种方法中,我们将遍历所有路径,并找到更新答案的最大弯道数。
示例
#include <bits/stdc++.h>
using namespace std;
struct Node { // 我们节点的结构
int key;
struct Node* left;
struct Node* right;
};
struct Node* newNode(int key){ // 初始化我们的节点
struct Node* node = new Node();
node->left = NULL;
node->right = NULL;
node->key = key;
return node;
}
void maximumBends(struct Node* node,char direction, int bends,
int* maxBends, int soFar,int* len){
if (node == NULL) // 如果达到 null
return;
if (node->left == NULL && node->right == NULL) { // 如果我们到达叶节点,则
//we check if we have to update our answer or not
if (bends > *maxBends) {
*maxBends = bends;
*len = soFar;
}
}
else {
if (direction == 'l') { // 当前方向为左
maximumBends(node->left, direction,bends, maxBends,soFar + 1, len);
maximumBends(node->right, 'r',bends + 1, maxBends,soFar + 1, len); // 如果我们改变方向,弯曲度也会增加
}
else {
maximumBends(node->right, direction,bends, maxBends,soFar + 1, len);
maximumBends(node->left, 'l',bends + 1, maxBends,soFar + 1, len); // 与 direction 为左时相同
}
}
}
int main(){
struct Node* root = newNode(10);
root->left = newNode(8);
root->right = newNode(2);
root->left->left = newNode(3);
root->left->right = newNode(5);
root->right->left = newNode(2);
root->right->left->right = newNode(1);
root->right->left->right->left = newNode(9);
int len = 0, bends = 0, maxBends = -1;
if(!root) // 如果树为空
cout << &";0\n";
else{
if (root->left) // 如果左子树存在
maximumBends(root->left, 'l',bends, &maxBends, 1, &len);
if (root->right) // 如果右子树存在
maximumBends(root->right, 'r', bends,&maxBends, 1, &len);
cout << len << "\n";
}
return 0;
}
输出
4
上述代码的解释
在上述方法中,我们只是遍历所有路径并计算到目前为止发现的弯道数。现在,当我们到达路径的末尾(即叶节点)时,我们会检查到目前为止的弯道数是否大于之前的最大值。如果条件为真,那么我们将最大弯道数以及路径长度更新为这个新长度,这就是我们的程序的运行方式。
结论
在本教程中,我们解决了一个问题,即找到具有最大弯道数的路径长度。我们还学习了这个问题的 C++ 程序以及我们解决这个问题的完整方法(普通方法)。我们可以用其他语言(如 C、java、python 和其他语言)编写相同的程序。我们希望您发现本教程很有用。


