计算幂 k 乘以 % m 的幂
data structurec++server side programming
我们的目标是计算幂 k 乘以 % m 的幂,输入基数、k 和 m 的值 −
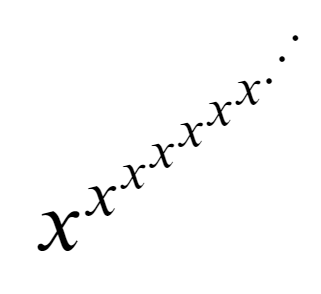
看上面的图片。你有没有试过计算这样的问题?让我们试试吧。
计算幂 k 乘以 % m 的幂,然后求与 m 的模。
解释
在这个问题中,给出了 x、k 和 m。计算 ${x^{x{^x{^{^.{^{^.{^{^.}}}}}}}}}$ 最多 k 次,然后与 m 取模。
让我们通过一个例子来理解。
给定 x = 2、k = 4 和 m = 6
因此,计算 $2^{2^{2{^2}}}\:=\:4^{2{^2}}\:=\:16^2\:=\:256$
然后 256 % 6 = 4。
因此,最终结果是 4。
方法
让我们讨论计算 k 次幂 % m 的幂的分步算法。
取 x、k 的值,和 m 作为输入。
使用 pow 函数计算 power 的幂,最后使用模数运算符获得最终结果。
将最终结果打印为输出。
C++ 程序计算 power k 乘以 % m 的幂。
#include <iostream>
#include <cmath>
using namespace std;
int powofpow(int x, int k){
int val = x;
k--;
while (k--)
val = pow(val, x);
return val;
}
int main(){
int x = 5, k = 2, m = 3;
int result;
result = powofpow(x, k);
result %= m;
cout << "Compute power of power " << k << " times % " << m << " of " << x << " is " << result << endl;
return 0;
}
输出
Compute power of power 2 times % 3 of 5 is 2
复杂度
时间复杂度:O(k),因为此代码执行了 (k-1) 次迭代。
空间复杂度:O(1),因为代码使用固定数量的变量来存储输入值和结果,而不管输入的大小如何。
结论
在本文中,我们尝试解释计算 k 乘以 % m 的幂的方法,其中基数、k 和 m 的值作为输入。我希望本文能帮助您更好地学习这个概念。


