二叉搜索树 - C++ 中的删除操作
c++server side programmingprogramming
二叉搜索树 (BST) 是一种特殊类型的树,它遵循以下规则 −
左子节点的值始终小于父节点注意
右子节点的值大于父节点。
所有节点单独形成二叉搜索树。
二叉搜索树 (BST) 的示例 −
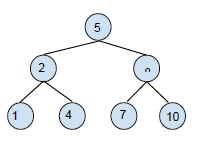
二叉搜索树是为了降低搜索、查找最小值和最大值等操作的复杂性而创建的。
删除操作二叉搜索树 (BST)
删除操作是从树中删除指定的节点。如果删除节点,有三种可能性 −
从树中删除叶节点:最简单的删除是从二叉搜索树中删除叶节点。删除叶节点时,只有叶受到影响。例如,

删除叶节点 7 可得到,
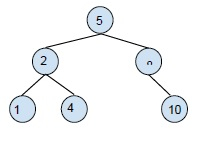
删除具有一个子节点的节点:对于此删除,您需要将子节点替换为要删除的节点,然后将其删除。例如,
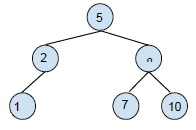
从 BST 中删除 2

删除具有两个子节点的节点:此处要删除的节点具有两个子节点。因此,我们将使用树的顺序形式,在这里我们将删除元素并选择其按顺序排列的邻居作为其位置并重新创建其余部分。例如,

从 BST 中删除 5 将返回以下树。

示例
#include<stdio.h>
#include<stdlib.h>
struct node{
int key;
struct node *left, *right;
};
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
void inordertraversal(struct node *root){
if (root != NULL){
inordertraversal(root->left);
printf("%d ", root->key);
inordertraversal(root->right);
}
}
struct node* insert(struct node* node, int key){
if (node == NULL) return newNode(key);
if (key < node->key)
node->left = insert(node->left, key);
else
node->right = insert(node->right, key);
return node;
}
struct node * minValueNode(struct node* node){
struct node* current = node;
while (current && current->left != NULL)
current = current->left;
return current;
}
struct node* deleteNode(struct node* root, int key){
if (root == NULL) return root;
if (key < root->key)
root->left = deleteNode(root->left, key);
else if (key > root->key)
root->right = deleteNode(root->right, key);
else{
if (root->left == NULL){
struct node *temp = root->right;
free(root);
return temp;
}
else if (root->right == NULL){
struct node *temp = root->left;
free(root);
return temp;
}
struct node* temp = minValueNode(root->right);
root->key = temp->key;
root->right = deleteNode(root->right, temp->key);
}
return root;
}
int main(){
struct node *root = NULL;
root = insert(root, 50);
root = insert(root, 30);
root = insert(root, 20);
root = insert(root, 40);
root = insert(root, 70);
root = insert(root, 60);
root = insert(root, 80);
printf("给定树的中序遍历 \n");
inordertraversal(root);
printf("\nDelete 20\n");
root = deleteNode(root, 20);
printf("修改后的树的中序遍历 \n");
inordertraversal(root);
printf("\nDelete 30\n");
root = deleteNode(root, 30);
printf("修改后的树的中序遍历 \n");
inordertraversal(root);
printf("\nDelete 50\n");
root = deleteNode(root, 50);
printf("修改后的树的中序遍历 \n");
inordertraversal(root);
return 0;
}
输出
给定树的中序遍历 20 30 40 50 60 70 80 Delete 20 修改后的树的中序遍历 30 40 50 60 70 80 Delete 30 修改后的树的中序遍历 40 50 60 70 80 Delete 50 修改后的树的中序遍历 40 60 70 80


