C++ 中的 Android 解锁模式
假设我们有一个 Android 3x3 键锁屏和两个整数 m 和 n,m 和 n 的值在 1 ≤ m ≤ n ≤ 9 范围内,我们必须计算 Android 锁屏的解锁模式总数,其中包含最少 m 个键和最多 n 个键。
规则是,每个模式必须连接至少 m 个键和最多 n 个键。所有键必须是唯一的。如果模式中连接两个连续键的线穿过任何其他键,则其他键必须先前在模式中被选中。不允许跳过任何未选中的键。所用密钥的顺序很重要。
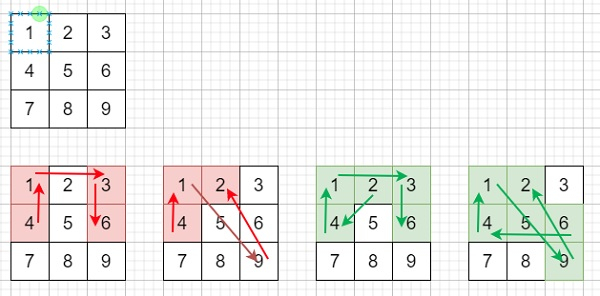
因此,如果输入为 m = 1、n = 1,则输出将为 9
为了解决这个问题,我们将遵循以下步骤 −
定义一个大小为 10 x 10 的数组 skip。
定义一个函数 dfs(),它将获取节点、len、访问的数组,
如果 len 与 0 相同,则 −
返回1
visited[node] := true
ret := 0
初始化 i := 1,当 i <= 9 时,更新(将 i 增加 1),执行 −
如果 visit[i] 为 false 且(skip[node, i] 与 0 相同或 visit[skip[node, i]] 非零),则−
ret := ret + dfs(i, len - 1, visited)
visited[node] := false
return ret
从 main 方法执行以下操作 −
用 0 填充 skip
skip[1, 3] := skip[3, 1] := 2
skip[1, 7] := skip[7, 1] := 4
skip[3, 9] := skip[9, 3] := 6
skip[7, 9] := skip[9, 7] := 8
skip[4, 6] := skip[6, 4] := skip[2, 8] := skip[8, 2] := skip[3, 7] := skip[7, 3] := skip[1, 9] := skip[9, 1] := 5
定义一个大小为 10 的数组 accessed
ret := 0
初始化 i := m,当 i <= n 时,更新(将 i 增加 1),执行 −
ret := ret + (dfs(1, i - 1, visited))
ret := ret + (dfs(2, i - 1, visited))
ret := ret + dfs(5, i - 1, visited)
return ret
示例
让我们看看下面的实现以便更好地理解 −
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
int skip[10][10];
int dfs(int node, int len, vector<bool>& visited){
if (len == 0)
return 1;
visited[node] = true;
int ret = 0;
for (int i = 1; i <= 9; i++) {
if (!visited[i] && (skip[node][i] == 0 || visited[skip[node][i]])) {
ret += dfs(i, len - 1, visited);
}
}
visited[node] = false;
return ret;
}
int numberOfPatterns(int m, int n){
memset(skip, 0, sizeof(skip));
skip[1][3] = skip[3][1] = 2;
skip[1][7] = skip[7][1] = 4;
skip[3][9] = skip[9][3] = 6;
skip[7][9] = skip[9][7] = 8;
skip[4][6] = skip[6][4] = skip[2][8] = skip[8][2] = skip[3][7] = skip[7][3] = skip[1][9] = skip[9][1] = 5;
vector<bool> visited(10);
int ret = 0;
for (int i = m; i <= n; i++) {
ret += (dfs(1, i - 1, visited) * 4);
ret += (dfs(2, i - 1, visited) * 4);
ret += dfs(5, i - 1, visited);
}
return ret;
}
};
main(){
Solution ob;
cout << (ob.numberOfPatterns(1,1));
}
输入
1, 1
输出
9

